有些数学问题表面上与一元二次方程无关,但是如果根据题目的特点,巧妙地构造一元二次方程来解(证),则更简洁明快,构造方程,即用已知条件作材料,用所求结论作变形方向,构造出一个方程形式,使得问题再现方程的观点下求解,体现数学的结构美.
一般而言,对于二次方程 ax1 ²+bx1+c=0 ,ax2 ²+bx2+c=0(a,b,c为常数且a≠0),其中的x1,x2 可看作方程 ax ²+bx+c=0(a≠0)的两根.
应注意其的前提是x1≠x2 ,这是因为当x1=x2时,x1与x2并不能完全保证是方程ax ²+bx+c=0 的两根,此时存在两种可能:
(1).方程 ax ²+bx+c=0 (a≠0)有两个相等的实数根 ,即 x =x1 =x2 ;
(2).方程 ax ²+bx+c=0 (a≠0)有两个不相等的实数根 ,其中x1,x2只是方程的其中一个根。
因而,在审题过程中必须看清是否有"x 1≠x2"这个条件,否则就会出现错误。常用构造一元二次方程的解题的策略如下:
类型一、利用根的定义构造:
若已知等式具有相同的结构,则可把某两个变元看做是关于某一个字母的一元二次方程的两根.
1.已知 p ²-2p-5=0 ,1/q ²-2/q-5=0,其中p,q为实数,且pq≠1,求p2+1/q ²的值。
解:易知q≠0 ,故由 pq≠1 可得p≠1/q ,
又 1/q ²-2/q-5=0 即 (1/q)2 -2(1/q)-5=0 与 p ²-2p-5=0 形式相同,
从而可知 p,1/q为方程 x2-2x-5=0的两根,
∴ p +1/q =2, p ·1/q =-5,
∴ p2+1/q ²=(p+1/q)2-2p·1/q = 4-2×(-5)= 4+10 = 14 。
方法点拨:上题中因为有 p≠1/q这个条件,因而可以逆用一元二次方程根的定义构造一元二次方程 x²-2x-5=0,从而利用韦达定理得解。
拓广变式:若把上题中的"pq≠1"这个条件去掉,将题目改为 " 已知 p²-2p-5=0,1/q ²- 2/q-5 =0,其中p,q为实数,求p²+1/q ²的值 ", 则解答过程应相应改为:
解:①、当p≠1/q时, p,1/q为方程 x² -2x-5=0 的两根,
∴ p+1/q =2, p·1/q =-5 ,
∴ p²+1/q ²=(p+1/q)² -2p·1/q = 4+10 = 14 。
②、当p = 1/q时,解p²-2p-5=0 得 p=1±√6 = 1/q ,
∴ p² + 1/q ²=2p² =2(1±√6)² = 14±4√6 ,
∴由 ①、②可知 p²+ 1/q ²的值为14或14+4√6或14-4√6。
类型二、确定主元构造:
对于含有多个字母的等式,可以将等式整理为关于某一个字母的一元二次方程.

即y=±1当y=1时,得x=±1;当y=-1时,无解.
故满足方程的所有整数对为(1, 1), (-1, 1).
3. 若a,b,c为实数,且a²+b²+c²-ab-bc-ca=0,求证:a=b=c.
证明 由已知等式,可构造关于c的一元二次方程c²-(a+b)c+(a²+b²-ab)=0.
∵c为实数,∴△=[-(a+b)] ²-4(a²+b²-ab)=-(a-b)²2≥0.
∵a,b为实数,∴(a-b) ²≥0,-3(a-b) ²≤0,
∴-3(a-b)²=0,∴a=b.同理可证b=c,∴a=b=c.
类型三、利用求根公式构造一元二次方程
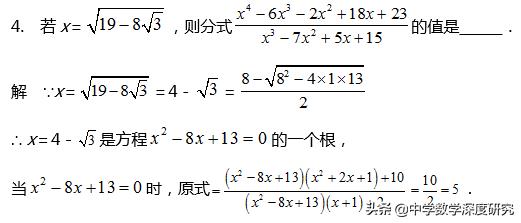
类型四、利用根与系数的关系构造:
若题目中出现形如x+y=a,xy=b的关系或隐藏着这种关系时,则
可看做是方程x²-ax+b=0的两实数根.
5. 假设x、y、z都是实数,且满足x+y+z=a, ①
x²+y²+z²=a²/2(a>0) ②
试证:x、y、z都不能是负数,也不能大于2a/3
证明:由①式得:x+y=a-z ③
由(③²-②)÷2得xy=(a/2 -z) ², ④
根据③、④构造一元二次方程t²-(a-z)t+(a/2-z) ²=0 ⑤
∵方程⑤有实根,
∴△=(a-z) ²-4(a/2-z) ²=-3z(z-2a/3) ≥0,
解这个关于
的一元二次不等式,得0≤z≤2a/3,
同理可证0≤x≤2a/3, 0≤y≤2a/3.
类型五、利用根的判别式构造:
若问题中出现形如△=b²-4ac的关系式时,可把a,b,c看做是一元二次方程的系数.
6. 已知(a-b) ²-4(b-c)(c-a)=0,求证:2c=a+b
简证:分两种情况讨论.
(1) 当b=c时,易得a=b=c,显然2c=a+b
(2) 当b≠c时,则可把b-c、a-b、c-a当做是有两个相等实数根的一元二次方程
(b-c)x²+(a-b)x+c-a=0的系数.
又∵(b-c)+(a-b)+(c-a)=0, ∴x1=x2=1,
由根与系数的关系得x1·x 2=(c-a)/(b-c)=1,即2c=a+b.
7. 已知n² (p-m) ²=4mp(m-n)(n-p),求证:1/m+1/m=2/p.
证明,由已知n² (p-m) ²=4mp(m-n)(n-p),
得n² (p-m) ²-4mp(m-n)(n-p)=0.
∴方程p(m-n)x²+n(p-m)x+m(n-p)=0(m≠n)有两个相等的实数根.
∵p(m-n)+n(p-m)+m(n-p)=0,
∴方程的两个实数根为x1=x2=1.
根据根与系数的关系,得1×1=m(n-p)/p(m-n)
化简得mn+np=2mp,∴1/m+1/m=2/p(m≠n)
当m=n时,由已知可得p=m,此时亦有1/m+1/m=2/p成立,
综上,1/m+1/m=2/p成立.
类型六、利用平方法构造:
利用已知量与所求量存在的平方关系构造.
8.利用平方根去根号可以构造一个整系数方程.例如:x=√2+1时,移项得x﹣1=√2,两边平方得(x﹣1)²=(√2)²,所以x²﹣2x+1=2,即x²﹣2x﹣1=0.仿照上述构造方法,当x=(√6- 1)/2时,可以构造出一个整系数方程是( )
A.4x²+4x+5=0B.4x²+4x﹣5=0C.x²+x+1=0D.x²+x﹣1=0
【解答】由题意可得:x=(√6- 1)/2,
可变形为:2x=√6﹣1,则(2x+1)=√6,故(2x+1)²=6,
则可以构造出一个整系数方程是:4x²+4x﹣5=0.
故选:B。
9. 若y=3-√6,求y²-6y+5的值.
解析:∵y=3-√6,∴y-3=-√6.
∴两边平方并整理得,y²-6y+3=0, ∴原式=( y²-6y+3)+2=2.
通过以上9个题目解答学习,我们应意识到构造一元二次方程解题作为一种数学思维方法,在解决某些数学问题时,若能充分挖掘题目中潜在的信息,构造与之相关的函数,将陌生问题转化为熟悉问题,可使问题顺利解决。

 加载中,请稍侯......
加载中,请稍侯......
精彩评论