解直角三角形有策略，学会这五点再也不难

解直角三角形是锐角三角函数知识的延伸与升华，是对直角三角形三边之间的关系、两锐角之间的关系，以及边角之间关系的系统梳理与灵活应用；同时，解直角三角形也是解决测量等方面问题的重要手段之一.事实上，无论多复杂的解直角三角形问题，最终都可以归结为对直角三角形除直角外的五个基本元素(三边和两锐角)之间关系的探究.本文撷取几例，谈谈解直角三角形的基本策略.

一、有“弦”用“弦”

例1 如图1，在Rt⊿ABC中，∠C=90°,斜边c=8,∠B=60°，求直角边b的长.

解析： 已知条件中给出斜边(即“弦”)c和锐角B，求∠B的对边b，故应使用∠B的正弦.

由sinB=b/c，得b=c×sinB=8×sin60°

评注：当已知直角三角形的一锐角和斜边(弦)，求此锐角的对边(或邻边)，或已知一锐角及其对边(或邻边)，求斜边(弦)时，应选用已知锐角的正弦(或余弦)关系式求解.即所谓有“弦”用“弦”.

二、无“弦”用“切”

例2 如图2，在Rt⊿ABC中，∠C=90°，a=30,∠B=30°,，求直角边b的长.

评注：当已知条件中未给出斜边(弦)，也不需要求斜边(弦)，即条件和结论仅与两直角边(勾、股)有关，而与斜边(弦)无关时，应选用已知锐角的正切(或余切)关系式求解.即所谓无“弦”用“切”.

三、宁“乘”毋“除”

例3　某条道路上通行车辆限速为60千米/时，在离道路50米的点P处建一个监测点，道路AB段为检测区(如图3).在⊿ABP中，已知∠PAB=29°,∠PBA=45°，一辆轿车通过AB段的时间为8. 2秒，请判断该车是否超速？

(参考数据：tan29°≈0.5543,tan61°≈1.8040,60千米/时=50/3米/秒)

评注 ：本例在求AC的长度时，采取将PC与∠APC相乘的方法，计算简单不易失误.其实，在求的AC长度时，亦可由tan∠APC=PC/AC,得AC=PC/tan∠APC=50/tan29°≈50/0.5543≈90.2(米).显然，与将PC和tan∠APC相乘求AC相比，若采用将PC与tan∠PAC相除的方法，计算既繁琐且易出错.故在解直角三角形时，在保证计算结果尽可能精确的前提下，如果既可以采取“相乘”，也可以采用“相除”的方法求直角三角形某条边的长度，一般应遵循宁“乘”毋“除”的原则.当然，某些只能采取“相除”的方法来解决的问题例外，见下例.

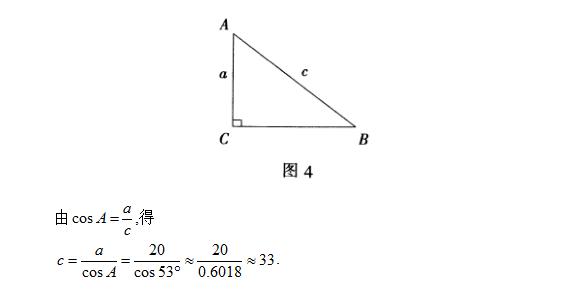
例4 如图4，在Rt⊿ABC中，∠C=90°,直角边a=20,∠A=53°，求斜边c (结果保留整数).(参考数据：sin53°≈0. 7986 ， cos53°≈0. 6018 ， tan53°≈1. 3270 )

解析： 解答此例，求斜边，显然只能采取“相除”的方法.

四、化“斜”为“直”

当已知条件为斜三角形的边和角时，往往需要通过适当添加辅助线构造出直角三角形，进而转化为解直角三角形的问题，上述例3即为此类题.兹再举一例.

例5 如图5，某直升机于空中A处测得正前方地面控制点C的俯角为30°;若航向不变，直升机继续向前飞行1000m至B处，测得地面控制点C的俯角为45°?求直升机再向前飞行多远，与地面控制点C的距离最近(结果保留根号).

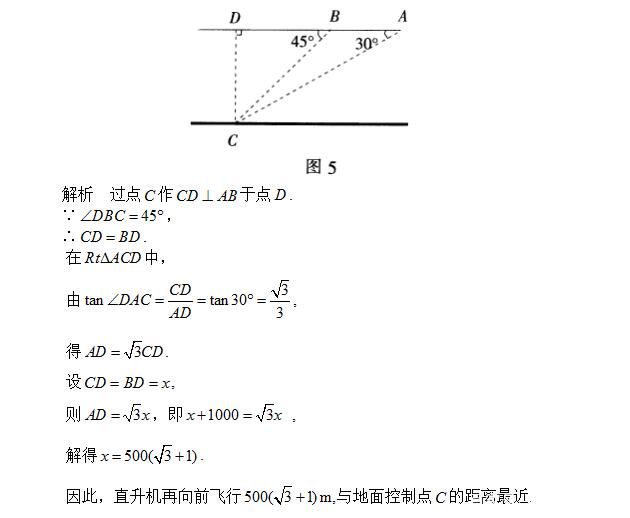
评注： 例3和例5是化“斜”为“直”的两个常见题型，可分别称为“求和”型、“求差”型.虽然化“斜”为“直”还有其他一些不同的变式，但与例3、例5相比，解题基本思路和方法并无二致，可谓万变不离其宗.

五、取“原”避“中”

例6 如图6，在Rt⊿ABC中，∠C=90°,斜边c=80，∠B=64°，求直角边a和b的长(精确到0.01).(参考数据：sin64°≈0. 8988 ，cos64°≈0. 4384 ， tan64°≈2. 0503)

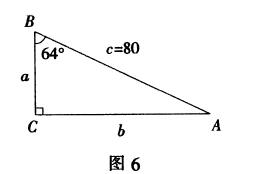
评注 ：上述解题过程中，在求出a的值以后，若由tanB=b/a，可得b=a×tanB=35.072×tan64°≈35.072×2.0503≈71.91.显然，这与析解中使用关系式“sinB=b/c”求得的b的值略有差异.其原因在于，借助“tanB=b/a”求b，此关系式中的a是中间数据，非原始数据，而析解中求b的值时所选数据均为原始数据，避开中间数据，所求结果无疑更为精确.此例告诉我们，在解直角三角形时，如果既可使用原始数据，也可使用中间数据，要尽量使用原始数据；即做到取“原”避“中”.