基本图形分析法：帮你分析角平分线和垂线的组合图形（十）

【分析方法导引】

当几何问题中，出现了角平分线和向角平分线所作的垂线的时候，就要想到可应用等腰三角形中重要线段的基本图形进行证明。

若角平分线的垂线没有过角的顶点时，可直接将角平分线的垂线延长到与角的两边相交，构成等腰三角形中重要线段的基本图形，然后再应用一次轴对称型全等三角形来完成分析。

若角平分线的垂线经过角的顶点时，则应将角平分线的垂线平行移动，使它离开角的顶点，然后再与角的两边相交构成等腰三角形中的重要线段的基本图形。

例16 如图3-175，已知：△ABC内接于⊙O，角平分线AD的延长线交⊙O于E，BF⊥AE，垂足是F。求证：AB^2-2BF^2=AB·AC—2AF·EF。

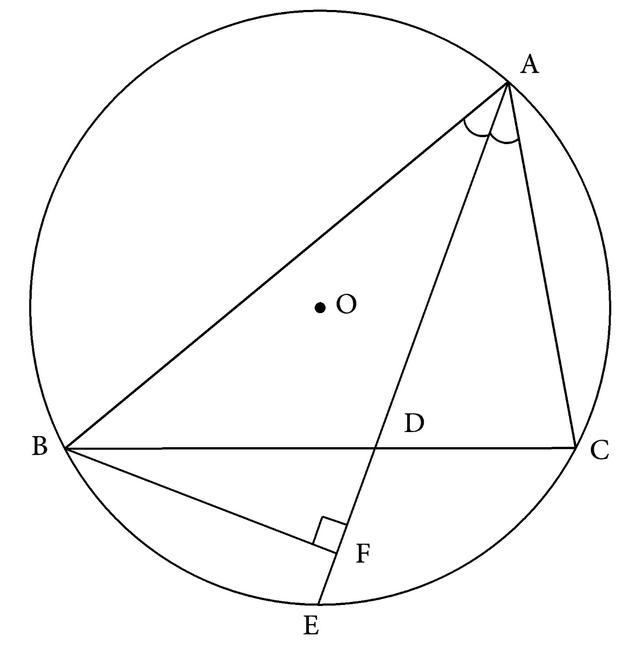
图3-175

分析：本题的条件中出现了BF是向角平分线AD作的垂线，所以必定会构成一个等腰三角形的基本图形。由于这个等腰三角形是由角平分线的垂线和角的两边相交得到的，所以延长BF交AC的延长线于G，并设BG交⊙O于H（如图3-176），即可得△ABF≌△AGF，AG=AB，BF=GF。

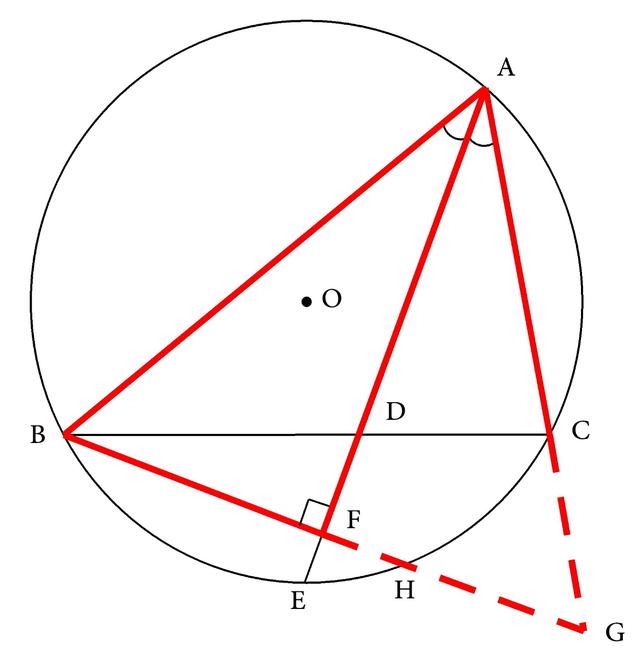
图3-176

本题要证明的结论由于等式两边都出现了AB，所以可先移项和提取因式转化为AB（AB-AC）=2BF^2-2AF·EF。而AB（AB-AC）=AG（AG-AC）=AG·CG。所以问题成为要证AG·CG=2BF^2-2AF·EF。对这一线段之间的比例关系式，我们首先也进行描图，以搞清楚比例关系之间的位置关系。经过描图，可以发现AG和CG这一组相乘线段重叠在一直线上，从而可应用逆平行线型相似三角形进行证明，由于现在出现的是由圆外一点G所作的圆的两条割线，所以可直接应用割线定理得AG·CG=BG·HG，而BG=2BF，HG=GF-HF，所以AG·CG=2BF（GF-HF）=2BF（BF-HF）=2BF^2-2BF·HF。将这个关系式与要证的结论相比较，即可得问题转化为要证AF·EF=BF·HF，但BH和AE是⊙O相交于F点的两条弦，所以直接应用相交弦定理就可证上述性质。

例17 如图3-177，已知：过⊙O外的一点P作⊙O的两条割线PAB、PCD，且分别与⊙O相交于A、B、C、D。PM是∠BPD的角平分线，AE⊥PM且分别交PD、⊙O于F、E，OG⊥PM垂足是G。求证：EF=2OG。

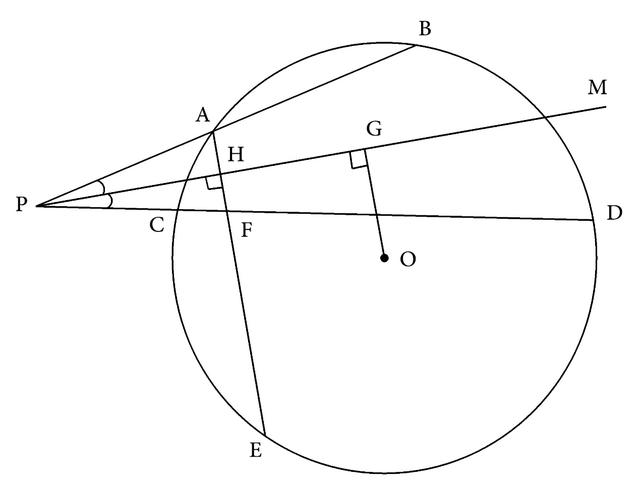
图3-177

分析：本题条件中出现AE是向角平分线PM所作的垂线，所以必定构成一个等腰三角形的基本图形。由AE与角的两边相交于A、F（如图3-178），就可得△APH≌△FPH，PA=PF，AH=FH。

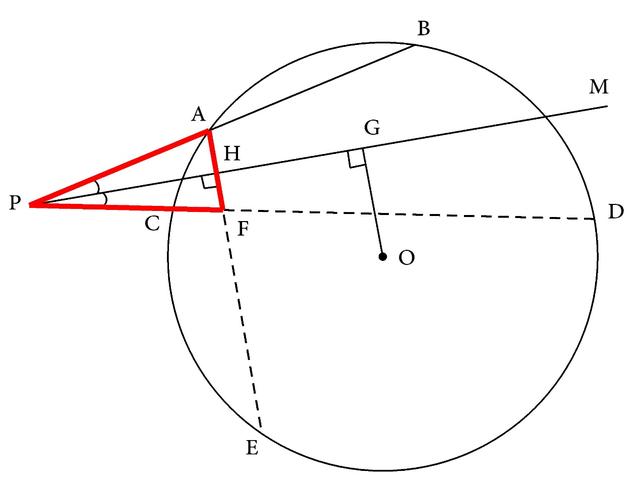
图3-178

由条件∠MHE=90°，而∠MHE是⊙O的一个圆内角，而圆内角的问题可以转化为圆周角的基本图形来进行讨论，转化的方法可以是过圆周角上的点作平行线。

若过A作PM的平行线交⊙O于K，则∠KAE=90°，这样就出现了90°的圆周角，从而就可以应用90°的圆周角的基本图形的性质进行证明，也就是∠KAE所对的弧是半圆，所对的弦是直径，而现在图形中是有圆周角而没有直径，所以应将直径添上，也就是联结EK后（如图3-179），必定有EK经过O点。

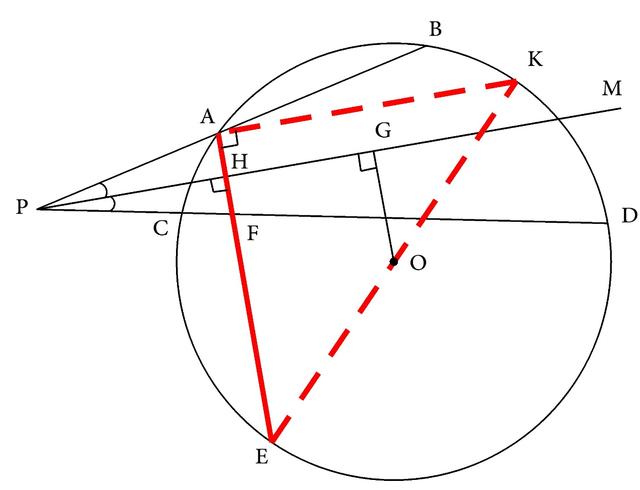
图3-179

由条件OG⊥PM和EA⊥PM，可得OG∥EA，且我们已经证明OE=OK，而要证得结论EF=2OG是线段之间的倍半关系，所以可应用三角形中位线的基本图形的性质进行证明。在△KAE中，过一边EK的中点O所作的另一边EA的平行线尚未和第三边AK相交，所以首先应将它们延长到相交，也就是延长OG交AK于N（如图3-180），即可得N是AK的中点，AE=2NO。

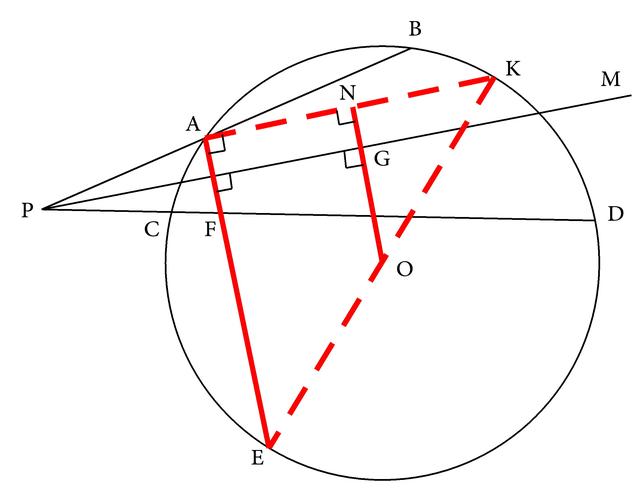
图3-180

而我们要证的是EF=2OG，于是上述性质可化为AF+EF=2（NG+OG）=2NG+2OG。将两式加以比较可知问题成为应证AF=2NG，而我们已证AF=2AH，所以问题进一步转化为应证AH=NG，由∠GNA=∠HGN=∠NAH=90°，四边形AHGN是矩形，当然就可以证明上述性质。

若过PM与⊙O的交点L作AE的平行线交⊙O于K，则∠MLK=90°，从而又进一步可得∠MLK所对的弦是直径，也就是联结KN后，必定有KN经过O点（如图3-181）。再由条件OG⊥PM，从而就可直接应用垂径定理，也就是设PM交⊙O于L、N，就有GL=GN，这样就出现了两个中点，是多个中点问题，就可以应用三角形中位线的基本图形的性质进行证明，于是就可得LK=2OG，而要证明的是EF=2OG，从而就是应证LK=FE，而我们已作LK∥FE，所以四边形LKEF就应是平行四边形，但这个四边形目前尚不完整，所以应先将它的一组对边添上，也就是联结LF、KF（如图3-181）。由于在这个四边形中LK=FE是要证明的结论，不能用，所以要证明这个四边形是平行四边形就只能转而证明LF和KE也平行。

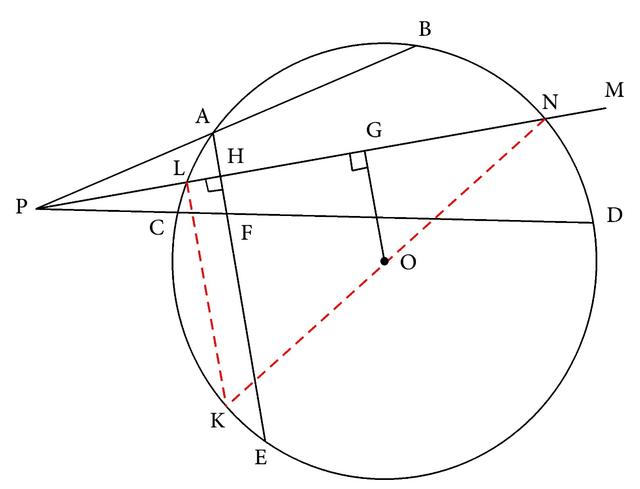
图3-181

由条件LK和AE是⊙O中的两条平行弦，应用平行弦的性质可得联结LA后有LA=KE，四边形LKEA是等腰梯形，所以∠E=∠LAF。又因为已证明PM是AF的垂直平分线，所以又可得∠LAF=∠LFA，那就可以证明∠LFA=∠E，LF∥KE，也就可以完成分析。

本题要证的结论EF=2OG是两条线段之间的倍半关系，所以可根据线段倍半关系的定义，作出OG的两倍，也就是延长OG到K，使KG=OG（如图3-182），那么问题就要证EF=OK。

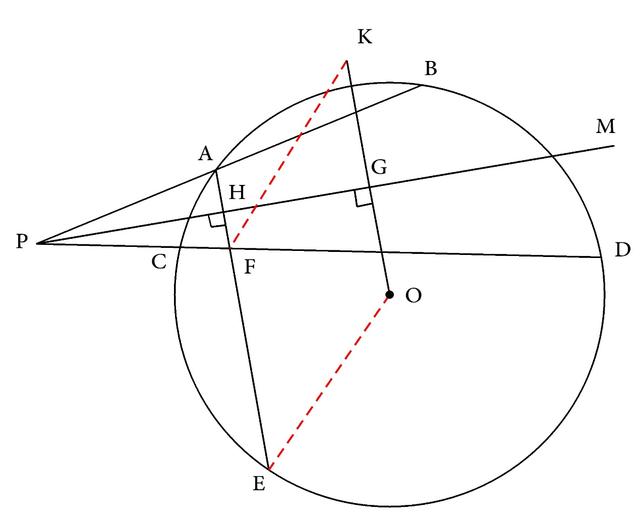
图3-182

由条件EF⊥PM，OK⊥PM，所以FE∥OK，这样就可以出现了EF和OK这两条线段不但相等，而且平行，所以它们可构成一个平行四边形，但这一个平行四边形目前还缺少一组对边，所以应先将这一组对边添上，也就是联结FK、EO（如图3-183），问题也就成为要证四边形FEOK是平行四边形。又因为EF和OK这一组对边相等是要证的结论，不能用，所以问题只能是证明另一组对边FK和EO也平行。由于FK和EO可以看作是被AE所截，所以问题就可转化为证∠E=∠AFK。

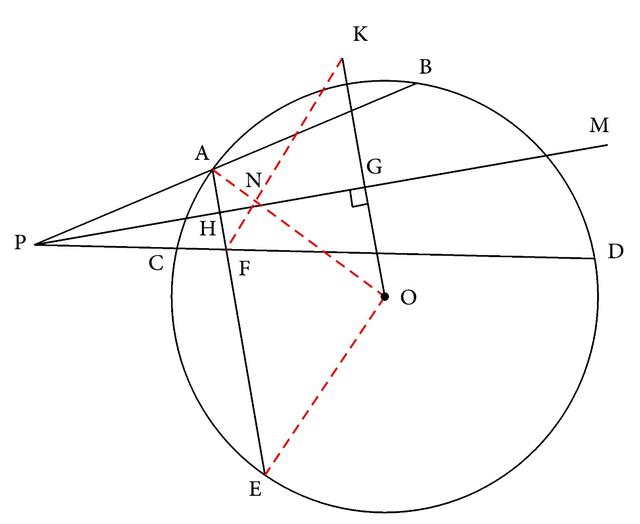
图3-183

由条件MP平分∠BOD和AF⊥PM，可得△PAH≌△PFH，AH=FH，PM就是AF的垂直平分线，于是设FK与PM相交于N，可得N在AF的垂直平分线上，所以又可以添加等腰三角形中重要线段的基本图形进行证明，添加的方法是将等腰三角形的腰添上，也就是联结NA（如图3-183），可得NA=NF，∠NAF=∠NFA，这样问题又转化为应证∠E=∠NAF。

又因为由条件PM⊥OK和所作的OG=KG，可得PM也是OK的垂直平分线，而N是PM上一点，所以可再一次添加等腰三角形中重要线段的基本图形进行证明，于是再联结NO（如图3-183）可得NO=NK，∠K=∠NOK，又因为已知AE∥KO，这一组平行线可以看作是被FK所截，所以∠AFK=∠K。这样就可得到在等腰△NAF和等腰△NOK中，它们的底角是相等的，所以它们的顶角也相等，即∠ANF=∠ONK，但已知F、N、K在一直线上，所以A、N、O也在一直线上，这样OA就是⊙O的半径，OA=OE，那就可证∠E=∠OAE，分析完成。