初二《全等三角形》数学模型之“一线三等角”模型

cc518学习网精品学习资料总目录

在初中数学《全等三角形》中有许多的模型，这些模型是数学重要知识点的总结与运用，很多几何题中都有数学模型的影子，掌握好这些模型，孩子们学习几何就会比较简单，成绩不会差。

今天我要与大家分享是“一线三等角”模型，那么什么是“一线三等角”？顾名思义，一线三等角是指三个相等的角的顶点在同一条直线上。这个模型贯穿初中几何的始终，初三讲《相似三角形》时这也是一个非常重要的知识点。下面我们具体分析一下这个模型。

例题一：如图∠1=∠2=∠3，且它们的顶点在直线AB上，这就是一个一线三等角模型。

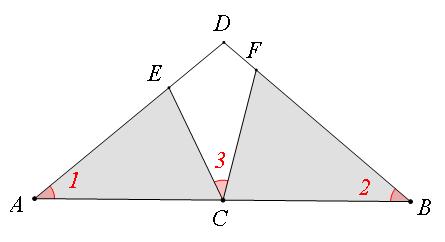
模型分析：

因为∠1=∠2=∠3，

所以：

∠ACE+∠AEC=∠CFB+∠BFC=∠ACE+∠BCF

易得：∠ACE=∠CFB，∠AEC=∠FCB

进而有△AEC∽△BCF（这是相似三角形一个重要的判定，我们将在初三学习），

如果再添加一组对应边相等，如CE=CF，或者是AE=BC，

那么就有△AEC≌△BCF.

模型性质总结

1、题目中只要满足“一线三等角”的条件，必相似；

2、题目如果两个条件：“一线三等角”和对应边相等的两个条件，必全等。

模型常见背景：

“一线三等角”的背景图形一般为正方形、等边三角形、等腰三角形等等。

1. 正方形ABCD，有一个直角的顶点在边AB上

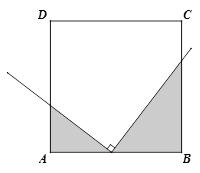
2. 等边三角形ABC，有一个60°角的顶点在边AB上

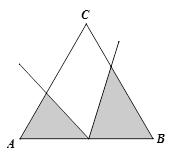
3. 等腰直角三角形ABC，有一个45°角的顶点在边AB上

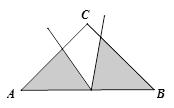
4.一线三直角

① ∠ACB＝90°，AD⊥CE，BE⊥CE

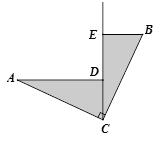
②AD⊥AC，EC⊥AC，DC⊥EC

典型例题

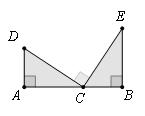
(1) 如图，已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，

CE⊥直线m，垂足分别为点D、E．证明：DE＝BD＋CE．

【解析】

∵BD⊥直线m，CE⊥直线m

∴∠BDA＝∠CEA＝90°

∵∠BAC＝90°

∴∠BAD＋∠CAE＝90°

∵∠BAD＋∠ABD＝90°

∴∠CAE＝∠ABD

又∵AB＝AC

∴△ADB≌△CEA

∴AE＝BD，AD＝CE

∴DE＝AE＋AD＝ BD＋CE；

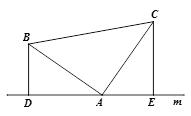
（2）如图，将(1)中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝a，其中a为任意锐角或钝角．请问结论DE＝BD＋CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

【解析】

（2）∵∠BDA＝∠BAC＝α

∴∠DBA＋∠BAD＝∠BAD＋∠CAE＝180°—α

∴∠DBA＝∠CAE

∵∠BDA＝∠AEC＝α，AB＝AC

∴△ADB≌△CEA

∴AE＝BD，AD＝CE

∴DE＝AE＋AD＝BD＋CE；

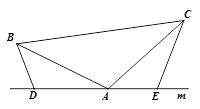
(3) 拓展与应用：如图，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状．

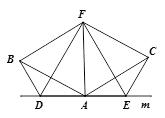
【解析】

（3）易知，△ADB≌△CEA，BD＝AE，∠DBA＝∠CAE，

∵△ABF和△ACF均为等边三角形

∴∠ABF＝∠CAF＝60°

∴∠DBA＋∠ABF＝∠CAE＋∠CAF

∴∠DBF＝∠FAE，∵BF＝AF

∴△DBF≌△EAF（如下图所示）

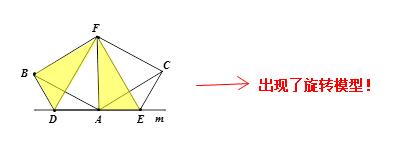
∴DF＝EF，∠BFD＝∠AFE

∴∠DFE＝∠DFA＋∠AFE＝∠DFA＋∠BFD＝60°

∴△DEF为等边三角形．

方法提炼

1 若题目中有一线三等角，可以直接证明相似或全等实现边与角的转化；

2 若题目中没有给出一线三等角，可以根据需要来构造。

综上所述，“一线三等角”是一个非常重要的模型，孩子们遇到这种情况时千万不要惊慌，就朝着三角形全等和相似考虑，肯定是没有问题的