「初中数学」一道二次函数题的思考

【题目呈现】

如图，已知抛物线y=ax²+bx+c(a≠0)的对称轴为直线x=一1，且经过A(1，0)，C(0，3)两点，与x轴的另一个交点为B.

(1)若直线y=mx+n经过B，C两点，求直线BC和抛物线的解析式;

(2)在抛物线的对称轴x=一1上找一点M，使点M到点A的距离与到点C的距离之和最小，求点M的坐标;

(3)设点P为抛物线的对称轴x=一1上的一个动点，求使△BPC为直角三角形的点P的坐标.

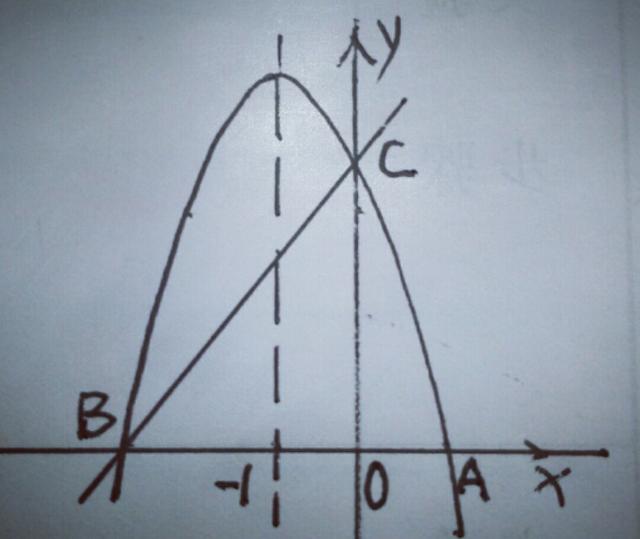
【分析】(1)利用待定系数法可求两函数的解析式，由于简单只写答案.抛物线的解析式为y=一x²一2x+3，直线BC的解析式为y=x+3.

(2)是典型的将军饮马问题.由于点A(1，0)与点B(一3，0)关于对称轴直线x=一1对称，则直线BC与直线×=一1的交点，就是使MA十MC最小的点M，∴把x=一1代入直线y=x+3，得y=2，∴所求的点M为(一1，2).

(3)这才是本文的重点，此问是二次函数背景下的直角三角形存在性问题，遇到此类问题该如何考虑呢？

【策略】抓住运动中的不变量，以不变应万变，万变不离其宗，充分研究题目中给定的信息，甚至挖掘"隐藏"的不变量，运用分类讨论的思想，转化的思想，使题目分类明确，转化信息，用已掌握的、熟练的方法来解决问题.本题中∠OBC=45°这个"隐藏"的信息非常有用.

【方法】常见的方法，大了说，就是:代数法与几何法.代数法，就是设出未知数，依据条件表示相关的量，进而列出方程进行求解.若题是多动点问题，代数法表示出相关的量可能未知数的次数高，或者未知数多，计算量大，理论上行得通，但考查上时间如金，往往不采用;若是单动点问题，相关的量已知或易于表示，未知数少易于解答同时分类简单明晰.几何法，能够很好的利用题中的信息，运用相关的定理，简化了计算量，但往往分类情况多且需一一画图，大多时候往往是代数，几何混合解题，既分类明晰，又计算简捷，体现了数与形的完善结合，正所谓，数缺形时少直观，形缺数时难入微。

【代数法】

设P点坐标为(一1，t)，又B点坐标为(一3，0)，C点坐标为(0，3)，∴BC²=18，PB²=(一1+3)²+t²=4+t²，PC²=(一1)²+(t一3)²=t²一6t+10.

若B为直角顶点，则BC²+PB²=PC²，即18+4+t²=t²一6t+10，解得t=一2;

若C为直角顶点，则BC²+PC²=PB²，即18+t²一6t+10=4+t²，解得t=4;

若P为直角顶点，则PB²+PC²=BC²，即4+t²+t²一6t+10=18，解得t1=3/2+√17/2，t2=3/2一√17/2.

综上所述，满足条件的点P共有4个，分别为(一1，一2)或(一1，4)或(一1，3/2+√17/2)或(一1，3/2一√17/2).

【几何法】

因点P在对称轴直线x=一1上，又由于△BPC为直角三角形，故可分三种情况讨论:

(一).当点B为直角顶点时，点P在直线BC下方的对称轴上，如图，

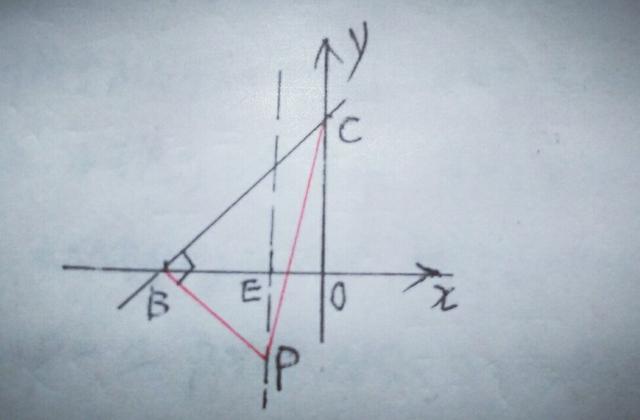
设对称轴x=一1与x轴交于E点，∵OB=OC=3，∴∠OBC=∠OCB=45°，紧抓这一不变量，而∠CBP=90°，∴∠PBE=45°，可得△BEP为等腰直角三角形，∴BE=PE=OB一OE=2，∴P点坐标为(一1，2).

(二)当点C为直角顶点时，点P为直线BC上方的对称轴上，如图

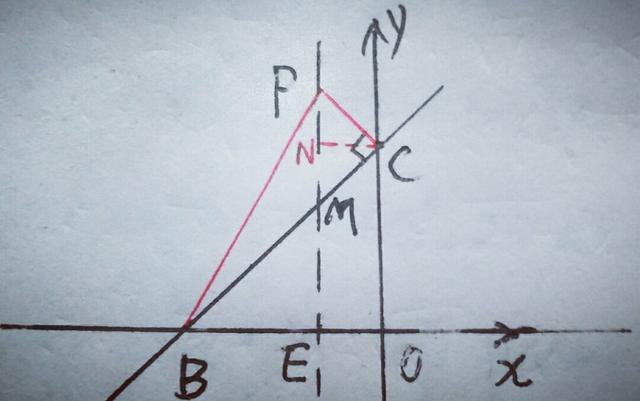
设对称轴直线x=一1与x轴交于点E，与直线BC交于点M，由于∠OBC=45°，则∠BME=∠CMP=45°，则△BEM为等腰直角三角形，BE=ME=2，过点C作CN⊥对称轴于N，则△CNM，与△PCM都是等腰直角三角形，∴PM=2CN=2，则PE=PM+EM=4，∴P点坐标为(一1，4).

(三)当点P为直角顶点时，点P可以在BC上方的对称轴上，也可在BC下方的对称轴上.

当点P在BC上方的对称轴上时，如图，

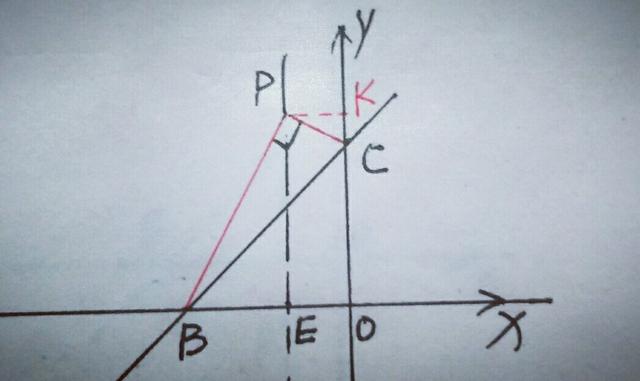
过点P作PK⊥y轴于K，由于△BEP，△PKC，△BOC都为直角三角形，可考虑用勾股定理解题，设P点坐标为(一1，t)，(t>3)，则KC=t一3，易知BE=2，PE=t，PK=1，∴BC²=OB²+OC²=BP²+CP²，而BP²=BE²+PE²，CP²=PK²+CK²，∴OB²+OC²=BE²+PE²+PK²+CK²，即3²+3²=2²+t²+1²+(t一3)²，解得t1=3/2+√17/2，t2=3/2一√17/2(舍去).∴P点坐标为(一1，3/2十√17/2).

另，可过P作MN∥x轴交y轴于N，过点B作y轴的平行线交MN于M，如图

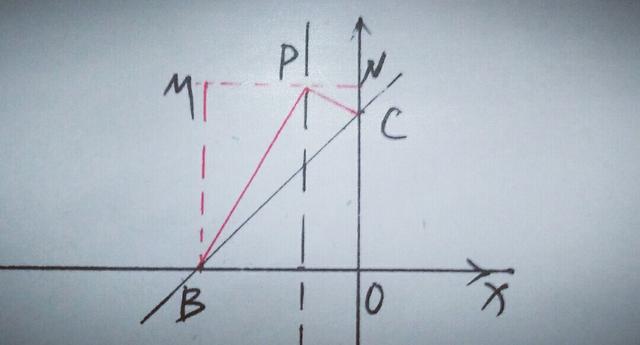
这时在MN这一条线上出现了三个直角，可用一线三垂直模型来解决，易知△MBP∽△NPC，设P点坐标为(一1，t)，则MP=2，PN=1，NC=t一3，MB=t，∴MB/PN=MP/NC，即t/1=2/(t一3)，∴t²一3t一2=0，解得t1=3/2十√17/2，t2=3/2一√17/2(舍去)，∴P点坐标为(一1，3/2+√17/2).

当点P在直线BC下方的对称轴上时，如图

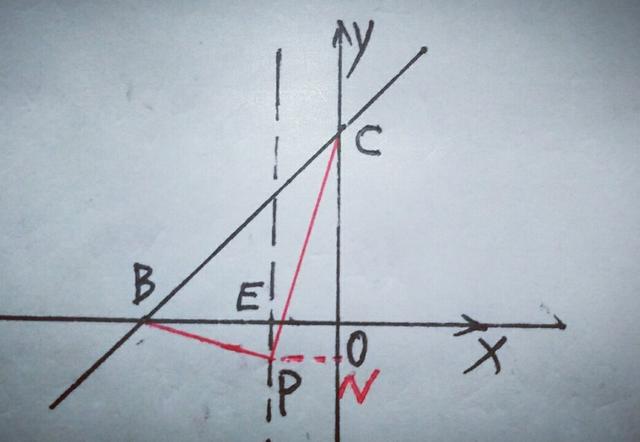
设对称轴与x轴交于E点，由于∠BCP<∠BCO=45°，∴∠CBP>∠CBO=45°，∴P点在E点下方，作PN⊥y轴于N，设P点坐标为(一1，t)，(t<0)，CN=3一t，易知BC²=BP²+PC²，BP²=BE²+EP²，PC²=PN²+CN²，∴BC²=BE²+EP²+PN²+CN²，即18=2²+(一t)²+1²+(3一t)²，解得t1=3/2一√17/2，t2=3/2+√17/2(舍去)，∴P点坐标为(一1，3/2一√17/2).

另，可过P作MN∥x轴交y轴于N，过B点作y轴的平行线交MN于M，如图

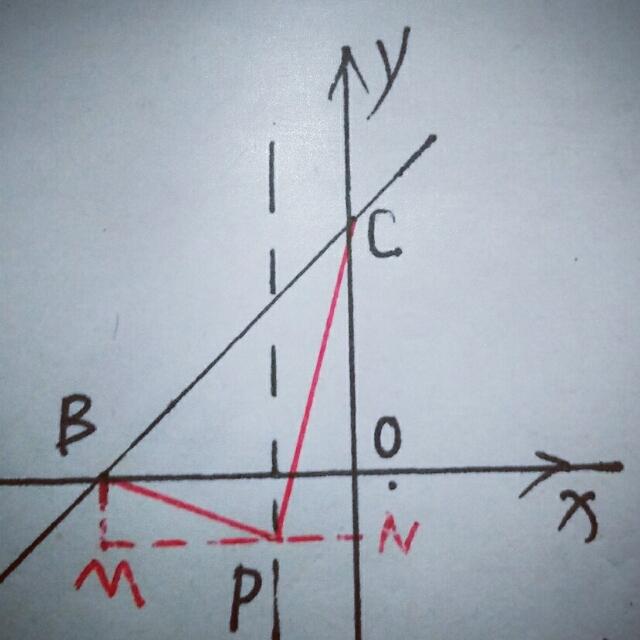
易知△MBP∽△NPC，设P(一1，t)，(t<0)，则MP=2，PN=1，NC=3一t，BM=一t，∴MB/PN=MP/NC，即一t/1=2/(3一t)，解得t1=3/2一√17/2，t2=3/2+√17/2(舍去)，∴P点坐标为(一1，3/2一√17/2).

综上，P点坐标为(一1，一2)或(一1，4)或(一1，3/2+√17/2)或(一1，3/2一√17/2).

【总结】代数法，几何法，各有千秋，一般相互结合甚是完美，同学们认真体会.