初中几何：巧用矩形的性质解题

矩形具有四个角都是直角、对边相等、对角线相等等性质，因此，充分利用这些性质可以解决与角、线段有关的问题.

【典例1】

已知：如下图所示，在矩形ABCD中，AC、BD是对角线，过顶点C作BD的平行线与AB的延长线相交于点E. 求证：△ACE是等腰三角形.

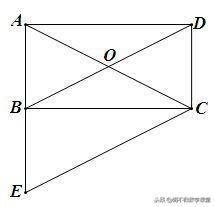
思路一：欲证△ACE是等腰三角形，即证AC=EC. 因AC、BD是矩形ABCD的对角线，则AC=BD，问题转化成证BD=EC. 只要说明四边形BECD是平行四边形即可.

思路二：欲证AC=EC，可证△ABC≌△EBC.由矩形性质可得∠ABC=∠EBC=90°，又因BC是公共边，需证AB=EB.由矩形性质可得AB=DC，再由平行四边形BDCE可得DC=EB，所以，AC=EC.

思路三：欲证AC=EC，需证∠CAE=∠E，因为CE∥BD，所以∠E=∠DBA，需证OA=OB.由矩形的性质就可得OA=OB.

点评：本题难度一般，主要提醒我们，对于特殊四边形问题，要善于充分挖掘特殊四边形的性质来求解，这是处理此类问题的重要方法，如方法一就是利用矩形、平行四边形的性质证明的；方法二和三，是综合运用三角形、特殊四边形的性质来求解.

【典例2】

已知：如下图所示，AB⊥BC，DC⊥BC，MA=MD，∠AMB=75°，∠DMC=45°，求证：AB=BC.

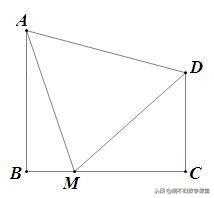
思路分析：题中的∠AMB=75°，∠DMC=45°有何用？实际是告诉你∠AMD=60°，又MA=MD，所以△AMD是等边三角形. 则AB所在的直角三角形中，另两个锐角分别为15°、75°，斜边为等边三角形的一边，要证AB=BC，需构造以BC为直角边且与△ABM全等的直角三角形.

证法一：如下图所示，过点D作DE⊥AB于E.，又∵ ∠B=∠C=90°，∴ 四边形BCDE是矩形. ∴ BC=ED.

∵ ∠AMD=180°-∠AMB-∠DMC=60°，MA=MD，∴ △AMD是等边三角形. ∵ ∠DAE=（90°-75°）+60°=75°，

∴ ∠AMB=∠DAE. 又∵∠B=∠AED，∴△ABM≌△DEA. ∴ AB=ED. ∴ AB=BC.

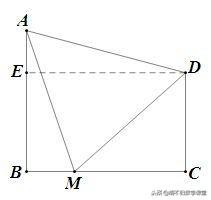
证法二：如下图所示，作AE⊥CD交CD的延长线于点E，又∵∠B=∠C=90°，∴四边形ABCE是矩形. ∴ BC=AE.

同证法一可得 △AMD是等边三角形，∴ ∠ADM=60°，∠CDM=90°-∠DMC=45°，∴ ∠ADE=75°.

∴ ∠AMB=∠ADE. 则△ABM≌△AED，∴ AB=AE. 又∵ AE=BC，∴ AB=BC.

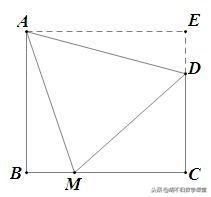
证法三：如下图所示，过点C作CE∥AD交AB于点E. 又因AE∥DC， 所以四边形AECD是平行四边形.

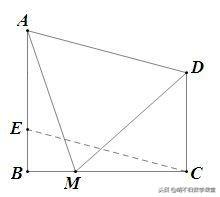
∵ AD∥CE，由证法一可知 △AMD是等边三角形，∴ AM=AD，∴ AM=CE. ∠BAM=90°-75°=15°.

∵ ∠CEB=∠DAB=∠BAM+∠MAD=75°，∴ ∠AMB=∠CEB. ∴ △ABM≌△CBE，∴ AB=BC.

点评：若需将一条线段平移到某一位置时，常可通过作垂线、平行线构造成矩形、平行四边形来实现.

【典例3】

已知：如下图，矩形ABCD中，AC、BD相交于点O，AE平分∠BAD，若∠EAO=45°，求∠BOE的度数.

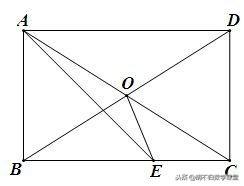
思路分析：∠BOE是△OBE的内角，要求∠BOE的度数，需求∠OBE、∠BEO，或找出它们与∠BOE的关系. 由题设可得∠OBE=∠ODA=∠OAD=30°，而∠BEO不易求出，因此，需找出∠BEO与∠BOE的关系.

【典例4】

已知：如下图，矩形ABCD中，延长CB到E，使CE=CA，F是AE的中点.求证：BF⊥DF.

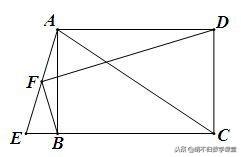
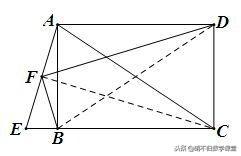
思路分析：如下图，连接CF、BD. 因为CE=CA，AF=FE，所以∠AFC=90°，要证BF⊥DF，需证∠DFB=∠AFC，因此只需证△FBD≌△FAC即可.