与函数零点有关的高考压轴题解题技巧
1.函数零点常与导数知识结合用于判断函数存在唯一 一个零点等命题.解题时常先判断函数在某区间上存在零点(存在性),再说明函数在相应区间上单调递增(或单调递减)即可(唯一性).
2.当题目不是求零点,而是利用零点的个数求参数的范围时,一般采用数形结合法.
利用导数解决与不等式有关的问题模板
处理双变量不等式问题,往往需要先经过适当的变形处理,以便灵活构造函数,并利用函数的单调性加以求解.破解此类题的关键点如下.
1.适当变形、灵活转化.结合题设条件,有时需要先对含有双变量的不等式进行“除法”变形,再对舍有双变量的局部代数式进行“换元”处理,将双变量问题等价转化为单变量问题;有时需要进行“移项”变形,从而使不等式两边具有相同的结构特点.
2.构造函数、利用导数.若转化为单变量问题,则可直接构造函数,并借助导数加以求解;若转化后不等式两边具有相同的结构特点,则可根据该结构特点构造函数,并借助导数加以求解.
经典例题:[2016·全国Ⅰ,21]
已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.
(1)求a的取值范围;
(2)设x1,x2是f(x)的两个零点,证明:x1+x2<2.
解析:(1)f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).
①设a=0,则f(x)=(x-2)ex,f(x)只有一个零点.
②设a>0,则当x∈(-∞,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0,所以f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增.
又f(1)=-e,f(2)=a,
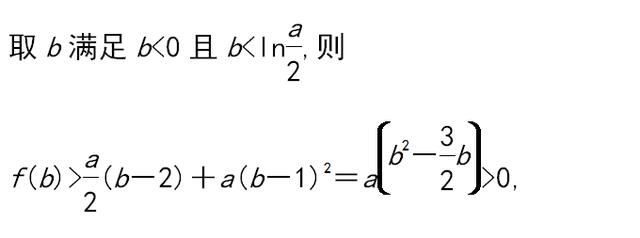
故f(x)存在两个零点.
③设a<0,由f′(x)=0得x=1或x=ln(-2a).
若a≥-e/2,则ln(-2a)≤1,故当x∈(1,+∞)时,f′(x)>0,因此f(x)在(1,+∞)上单调递增.
又当x≤1时,f(x)<0,所以f(x)不存在两个零点.
若a<-e/2,则ln(-2a)>1,
故当x∈(1,ln(-2a))时,f′(x)<0;当x∈(ln(-2a),+∞)时,f′(x)>0,因此f(x)在(1,ln(-2a))上单调递减,在(ln(-2a),+∞)上单调递增.
又当x≤1时,f(x)<0,所以f(x)不存在两个零点.
综上,a的取值范围为(0,+∞).
(2)不妨设x1<x2.由(1)知,x1∈(-∞,1),x2∈(1,+∞),2-x2∈(-∞,1),f(x)在(-∞,1)上单调递减,所以x1+x2<2等价于f(x1)>f(2-x2),即f(2-x2)<0.
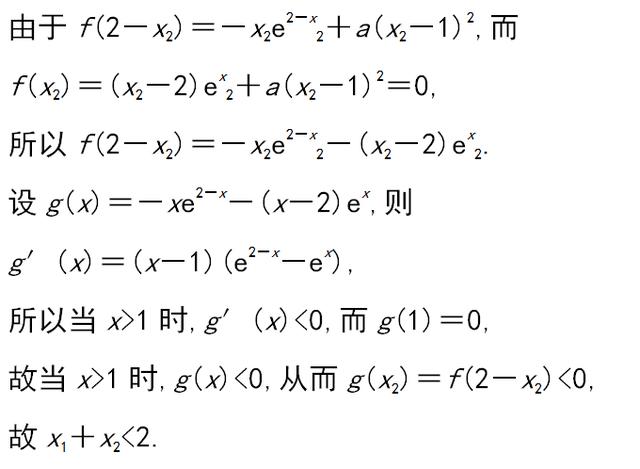

 加载中,请稍侯......
加载中,请稍侯......
精彩评论