「初中数学」相似三角形与函数的综合应用

相似三角形与函数的综合题综合性较强，是中考压轴题之一，解题时常运到方程思想，分类思想进行解答.

一.相似三角形与一次函数的综合

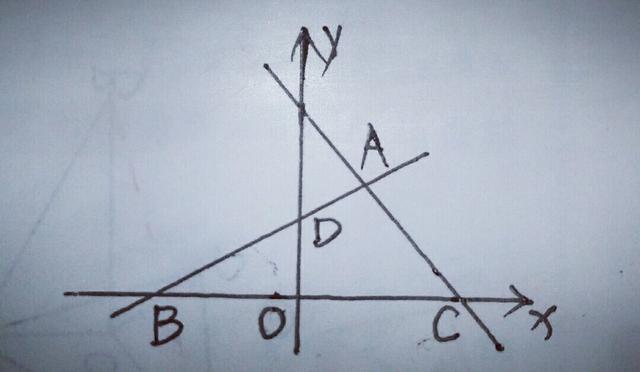
1.如图，在平面直角坐标系中，直线y=一x+3与x轴交于点C，与直线AD交于点A(4/3，5/3)，点D的坐标为(0，1).

(1)求直线AD对应的函数解析式;

(2)直线AD与x轴交于点B，若点E是直线AD上一动点(不与点B重合)，当△BOD与△BCE相似时，求点E的坐标.

【分析】(1)由A，D两点利用待定系数法可求直线AD对应的函数解析式为y=x/2+1.

(2)首先△BOD是直角三角形，要使△BCE与△BOD相似，则△BCE必是直角三角形，而∠B共用，所以可分∠BEC与∠BCE两种情况讨论，如图

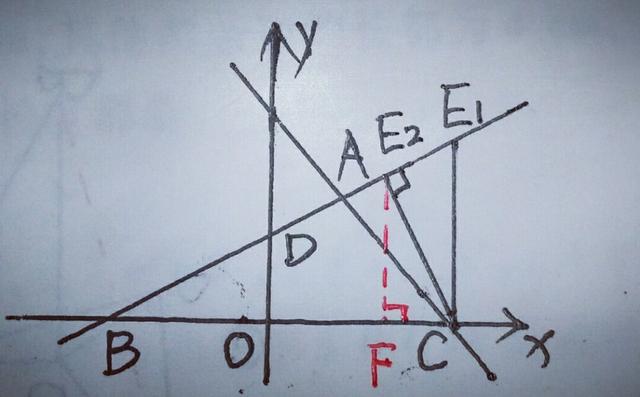
由(1)知直线AD的解析式为y=x/2+1，∴可得B点坐标为(一2，0)，由于直线AC的解析式为y=一x+3，∴可得C点坐标为(3，0)，∴BC=5，设E点坐标为(x，x/2+1)，

①当E1C⊥BC时，△BOD∽△E1BC，此时点C和点E1横坐标相同，将x=3代入y=x/2+1，解得y=5/2，∴E1(3，5/2).

②当CE2⊥AD时，△BOD∽△BE2C，过点E2作E2F⊥x轴于点F，易知∠E2BF=∠CE2F，∴.△E2BF∽△CE2F，∴E2F/BF=CF/E2F，即E2F²=CF×BF，∴(x/2+1)²=(3一x)(x+2)，解得x1=2，x2=一2(舍去)，∴E2(2，2).

综上所述，点E坐标为(3，5/2)或(2，2)

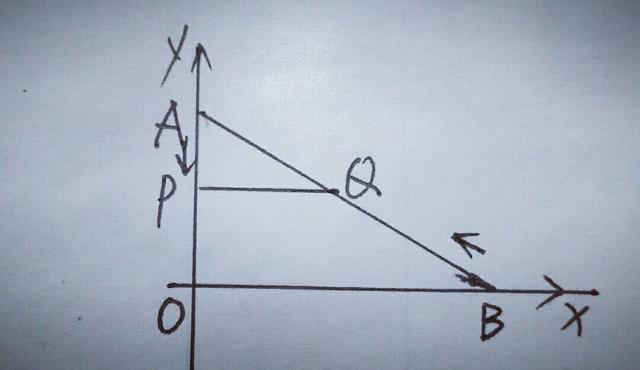
2.如图，在平面直角坐标系中，A(0，6)，B(8，0)，动点P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P，Q移动的时间为t(s).

(1)求直线AB对应的函数解析式;

(2)当t为何值时，△APQ与△AOB相似？

【分析】(1)设出直线AB的函数解析式y=Kx+b，用待定系数法可求出，为y=一3x/4+6.

(2)由于∠BAO是△APQ和△AOB的公共角，所以AP，AQ和AO，AB，对应边的比有两种情况，分类求出t的值.由AO=6，BO=8，可得AB=10，则AP=t，AQ=10一2t，如图，

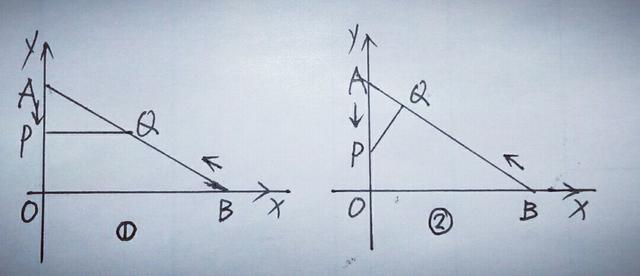
①如图①，当AP/AO=AQ/AB时，△APQ∽△AOB，∴t/6=(10一2t)/10，解得t=30/11.

②如图②，当AP/AB=AQ/AO时，△AQP∽△AOB，∴t/10=(10一2t)/6，解得t=50/13.

综上可得，当t=30/11或50/13时，△APQ与△AOB相似.

二.相似三角形与二次函数的综合

3.如图，直线y=2x+2与x轴交于点A，与y轴交于点B，把△AOB沿y轴翻折，点A落到点C，过点B的抛物线y=一x²+bx+C与直线BC交于点D(3，一4).

(1)求直线BD和抛物线对应的函数解析式.

(2)在第一象限内的抛物线上，是否存在一点M，作MN垂直于x轴，垂足为点N，使得以M，O，N为顶点的三角形与△BOC相似？若存在，求出点M的坐标;若不存在，说明理由.

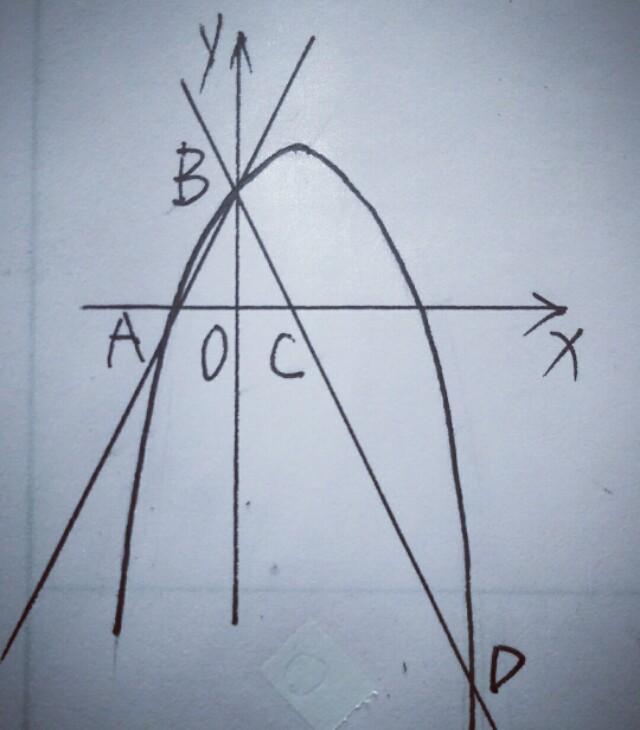
【分析】(1)由直线y=2x+2与y轴交于B点，可得B点坐标为(0，2)，与X轴交于A点，可得A点坐标为(一1，0)，又C点与A点关于y轴对称，可得C点坐标为(1，0)，又D点坐标为(3，一4)∴可得直线BD的解析式为y=一2x+2，把B(0，2)，D(一3，4)代入y=一x²+bx+c，可得抛物线对应的函数解析式为y=一x²+x+2.

(2)由于M点在第一象限，且MN⊥x轴于N，∴△MON与△BOC相似有两种情况，如图

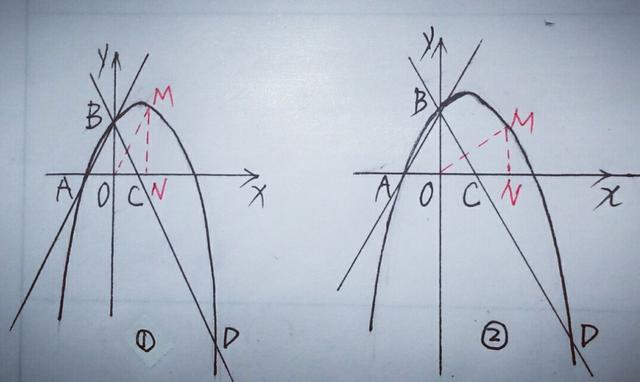
①如图①，当△MON∽△BCO时，ON/OC=MN/OB，即ON/1=MN/2，∴MN=2ON，设ON=a，则MN=2a，∴M点坐标为(a，2a)，代入抛物线解析式，得一a²+a+2=2a，解得a1=一2(不合题意，舍去)，a2=1，∴M(1，2).

②如图②，当△MON∽△CBO时，ON/OB=MN/OC，即ON/2=MN/1，∴MN=ON/2，设ON=b，MN=b/2，∴M点坐标为(b，b/2)，代入抛物线的解析式得，一b²+b+2=b/2，解得b1=1/4一√33/4(不合题意，舍去)，b2=1/4十√33/4，∴M(1/4十√33/4，1/8+√33/8)，所以存在这样的点M(1，2)或(1/4+√33/4，1/8+√33/8).

4.如图所示，已知点A(一2，4)和点B(1，0)都在抛物线y=mx²+2mx+n上.

(1)求m，n;

(2)向右平移抛物线，记平移后点A的对应点为A'，点B的对应点为B'，若四边形AA'B'B为菱形，求平移后抛物线的表达式;

(3)记平移后抛物线的对称轴与直线AB'的交点为C，试在x轴上找一D，使得以点B'、C、D为顶点的三角形与△ABC相似.

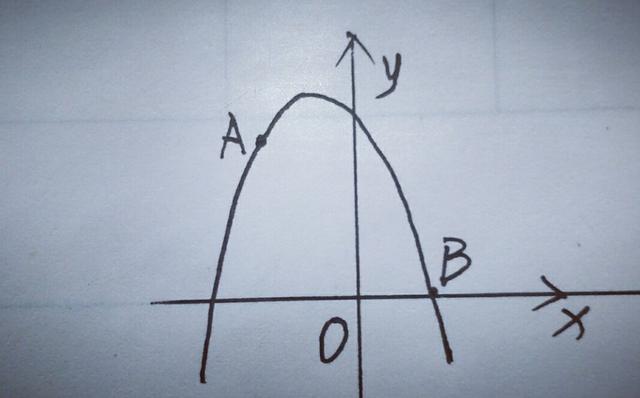
【分析】(1)将A(一2，4)和B(1，0)代入抛物线解析式y=mx²+2mx+n，得出m=一4/3，n=4.

(2)由于四边形AA'B'B是菱形，则AA'=BB'=AB=5，由抛物线解析式y=一4x²/3一8/3x+4=一4/3(x+1)²+16/3，∴向右平移5个单位的抛物线解析式为y'=一4/3(x一4)²+16/3.

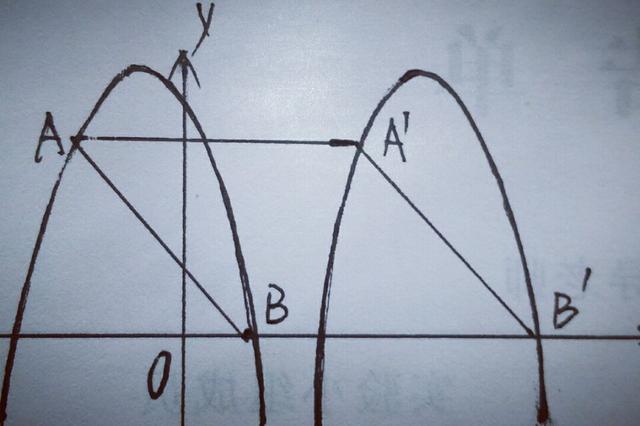
(3)设D(x，0)，依题意得，C(4，1)，AB=5，AC=3√5，BC=√10，B'C=√5，∵∠A=∠BB'A，所以分两种情况，如图，

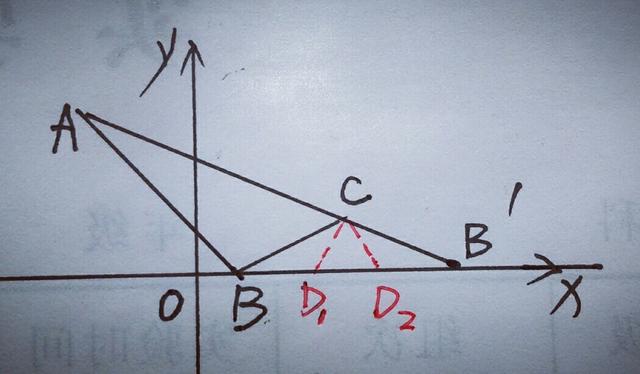
①△ABC∽△B'CD时，记D为D1，∠ABC=∠B'CD1，B'D=6一x，由AB/B'C=AC/B'D，得5/√5=3√5/(6一x)，解得x=3，∴D1(3，0).

②△ABC∽△B'DC时，记D为D2，AB/B'D=AC/B'C，5/(6一x)=3√5/√5，解得x=13/3，∴D2(13/3，0).

综上所知，D点坐标为(3，0)或(13/3，0).

三.相似三角形与反比例函数的综合

5.如图，矩形OABC的顶点A，C分别在x轴和y轴上，点B的坐标为(2，3)，双曲线y=K/x(x>0)经过BC的中点D，且与AB交于点E，连接DE.

(1)求K的值及点E的坐标;

(2)若点F是OC边上一点，且△FBC∽△DEB，求直线FB对应的函数解析式.

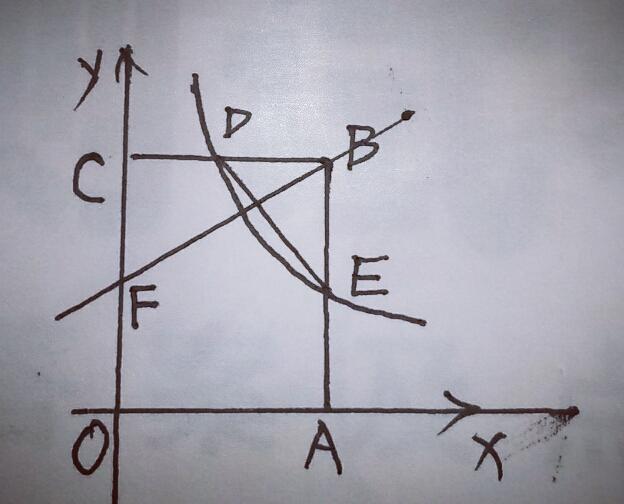
【分析】(1)由B点坐标(2，3)可知D点坐标为(1，3)，∴K=1×3=3，则双曲线解析式为y=3/x，∵E在AB上，∴其横坐标为2，又E在双曲线上，∴可得纵标为3/2，∴E点坐标为(2，3/2).

(2)由于D是BC的中点，可知BD=1，又可知BE=AB一AE=3一3/2=3/2，CB=2，∵△FBC∽△DEB，∴BD/CF=BE/CB，∴CF=4/3，∴OF=5/3，∴F点坐标为(0，5/3)，则可求FB的解析式为y=2x/3+5/3.

6.如图，在矩形OABC中，OA=3，OC=5，分别以OA，OC所在直线为x轴，y轴建立平面直角坐标系，D是BC上的一个动点(不与C，B重合)，反比例函数y=K/x(K>0)的图象经过点D，且与边BA交于点E，连接DE.

(1)连接OE，若△EOA的面积是2，则K的值是多少？

(2)连接CA，DE与CA是否平行？说明理由.

(3)是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标;若不存在，说明理由.

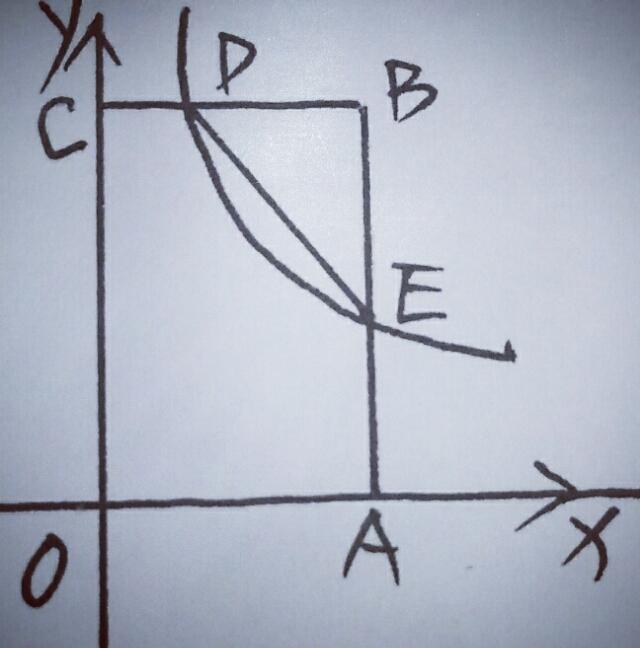
【分析】(1)由△EOA的面积为2，∴|K|/2=2，∴K=±4，又∵K>0，∴K=4.

(2)如图，要分析DE是否与CA平行，从条件看，用相似合理，况且由于D，E两点都在双曲线上，K相等，从图看，CD×AB=OA(或BC)×AE=|K|，即CD:BC=AE/AB，为相似提供了条件(这一点同学们一定要牢记).

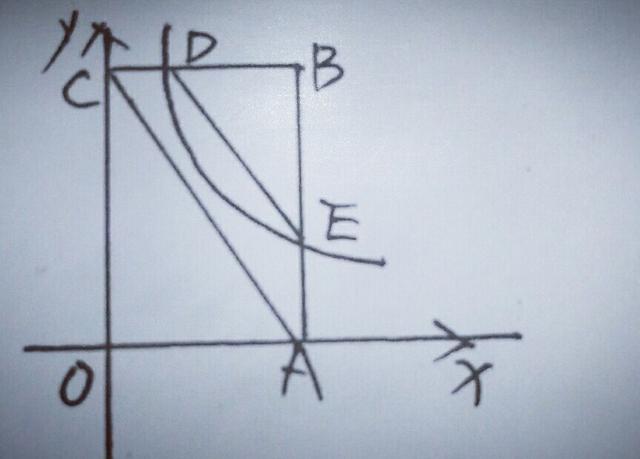
设D点坐标为(K/5，5)，E点坐标为(3，K/3)，则CD:CB=K/5:3=K:15，AE:AB=K/3:5=K:15，∴CD:CB=AE:AB，∴BD:CB=BE:AB，又∠DBE=∠CBA，∴△BDE∽△BCA，∴∠BDE=∠BCA，∴DE∥AC.

(3)假设存在点D，使得点B关于DE的对称点F在OC上，过E点作EG⊥OC于G，如图

出现了K型图，易知△CDF∽△GFE，此时FD=BD，EF=BE，设D点坐标为(K/5，5)，E点坐标为(3，K/3)，由(2)知，CA∥DE，BD:CD=BE:AE，∴BD:BE=CD:AE=3:5，设CD=3t，AE=5t，而△CDF∽∴GFE，∴CD:GF=DF:EF=CF:GE=BD:BE=3:5，∴可得GF=5CD/3=15t/3，CF=3GE/5=9/5，∴GF+CF+OG=15t/3+9/5+5t=5，解得t=8/25，∴CD=3t=24/25，这样通过建立方程求出CD，说明存在符合条件的D点，D点坐标为(24/25，5).