初中数学“定角对动弦”类的问题你听说过吗

首先，我们来看一道例题。

例1：如图∠BAC=60°，半径长为1的⊙O与∠BAC的两边相切，P为⊙O上一动点，以P为圆心，PA长为半径的圆交射线AB、AC于D、E两点，连接DE，则线段DE长度的最大值为 ，最小值为 .

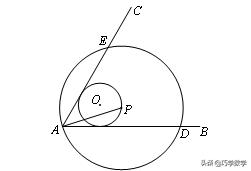
【分析】在这道题当中，首先角bac的度数是一定的，由于点p在圆o上运动，所以AP的长，是在不断发生变化的，因此圆p的半径在发生变化，从而DE的长度也会发生改变。由于角BAC是圆p的圆周角，它的度数是60度，因此，根据圆周角定理，可以知道角DPE的度数始终是120度。从而弦DE的长，始终等于圆p半径的根号3倍。所以，当圆p的半径最大时，DE长也最大，当圆p的半径最小时，DE长也最小。

【简答】连接PE、PD，过P作PH⊥DE与H，则EH=DH，∠DPH=60°，

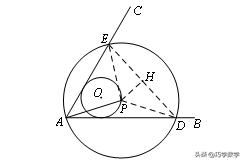
【总结】从这道题当中我们可以学习到，定角所对的弦是运动的时候，仍然可以利用隐形圆去解决。对比我们之前讲过的定弦对定角的问题，可以发现，当题目中出现定角对定弦时，隐形圆的半径是固定的，若定角所对的弦是动弦，那么隐形圆的半径是变化的，所得到的圆是一个动态圆，但是我们仍然不要害怕，动态问题可以静态的去分析，利用已知条件和圆的相关知识，找到所求与已知的等量关系去解决这样的问题。

下面我们来看一下例2。

例2：已知矩形ABCD中，AB=√3，BC=3，动点E、F分别在AC、BC上，且∠ABE=∠BFE，则BF的最小值是 .

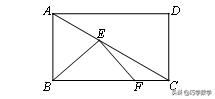
【分析】∵∠ABE=∠BFE，∴∠BFE+∠EBF=∠ABE+∠EBF=90°，∴∠BEF=90°，

B、E、F三点可看做在以BF为直径的⊙O上，直径BF是变化的，属于定角动弦类隐形圆模型。要使BF最小，只需OE最小，若O是定点，那么当OE⊥AC时，OE最小，则BF也最小，但此题中，随着E点的运动，F点是运动的，从而O点也是运动的，就不能直接说当OE⊥AC时，OE最小.

【简答】我们可以这么做：过O点作OH⊥AC于H，则△OHC∽△ABC，

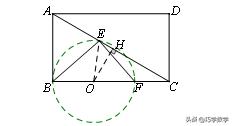
【总结】在这道题当中，我们应该很容易能够做出这个隐形圆，再利用直角三角形当中斜边大于直角边这样的一个思想，巧妙的，严谨的解决这道题。