例题1

已知：如图，在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F。

求证：∠DEN=∠F。

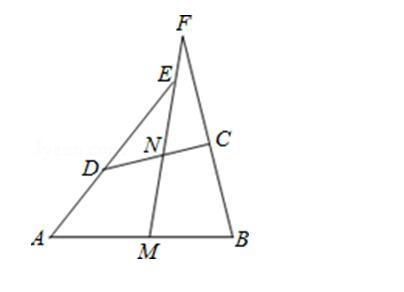
1、利用题目中的条件，合理添加辅助线

根据题目中的条件：M、N分别是AB、CD的中点，考虑添加辅助线构造三角形的中位线，由三角形的中位线定理，可以得到线段之间的平行关系和线段之间的数量关系。根据平行线的性质，利用同位角、内错角之间的关系，将结论需要证明的两个有相等关系的角转换到同一个三角形中，只要证明到这个三角形为等腰三角形，就可以根据等腰三角形的性质，判定这两个角相等。

因此，这样添加辅助线：连接AC，取AC的中点P，连接DP、MP。

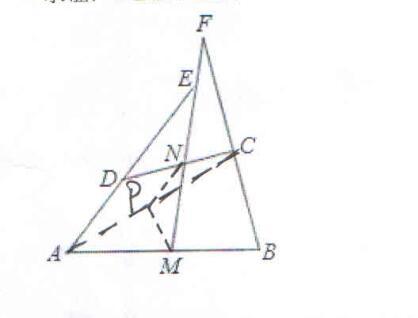
2、利用中位线、平行线的性质，把需要证明的结论进行转换

根据题目中的条件和辅助线：N是CD的中点，P是AC的中点，则NP是△CDA的中位线；

根据三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半，则NP∥AD，NP=AD/2；

同理，可证明得：MP∥BC，MP=BC/2；

由结论：NP∥AD，根据平行线的性质：两直线平行，同位角相等，则∠DEN=∠PNM；

由结论：MP∥BC，根据平行线的性质：两直线平行，内错角相等，则∠F=∠PMN。

3、利用等腰三角形的性质和等量替换，得到需要证明的结论

根据结论和条件：NP=AD/2，MP=BC/2，AD=BC，则NP=MP；

根据等腰三角形的性质：等边对等角，则∠PNM=∠PMN；

根据结论：∠DEN=∠PNM，∠F=∠PMN，∠PNM=∠PMN，则∠DEN=∠F。

例题2

如图，分别以△ABC的边AC、BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到AB的距离是AB的一半。

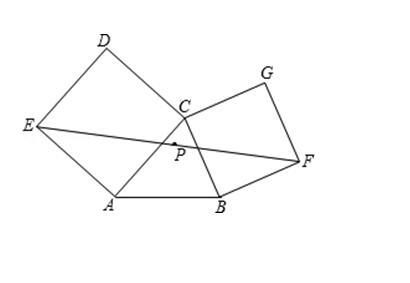
1、结合题目中的条件和需要证明的结论，合理添加辅助线

根据题目中的条件和需要证明的结论：点P是EF的中点，点P到AB的距离是AB的一半，考虑添加辅助线，构造梯形和中位线，利用梯形的中位线定理：梯形的中位线是上底与下底和的一半，可以得到点P到AB的距离与梯形上下底的关系。再考虑添加辅助线，把△ABC 和AB分为两部分，得到两个三角形和两条线段，利用全等三角形的性质：对应边相等，把AB分为的两条线段分别转换为梯形的上下底，从而得到需要证明的结论。

因此，这样添加辅助线：过P点作PM⊥AB，交AB于M点，过F点作FT⊥AB，交AB的延长线于T点，过E点作ES⊥AB，交AB的反向延长线于S点，过C点作CN⊥AB，交AB于N点。

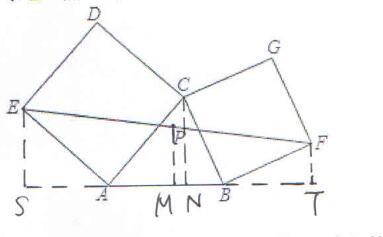
2、利用辅助线和题目中的条件，证明三角形全等

根据辅助线：CN⊥AB、FT⊥AB，则△CBN和△BFT为直角三角形，即∠CBN+∠NCB=90°；

根据题目中的条件：四边形BCGF为正方形，则CB= BF，∠CBF=90°；

根据题目中的条件和结论：∠CBN+∠CBF+∠FBT=180°，∠CBF=90°，则∠CBN+∠FBT =90°；

由结论：∠CBN+∠NCB=90°，∠CBN+∠FBT =90°，根据同角的余角相等，则∠NCB =∠FBT；

同理，可证明得∠CBN =∠BFT；

由结论：∠NCB =∠FBT，CB= BF，∠CBN =∠BFT，根据三角形全等的判定（ASA），则△CBN ≌△BFT。

3、利用全等三角形的性质和中位线定理，得到需要证明的结论

根据全等三角形的性质：全等三角形的对应边相等，则BN=FT；

同理，可证明得：AN=ES；

根据结论：BN=FT，AN=ES，AB=AN+BN，则AB=AN+BN=ES+FT；

由辅助线：PM⊥AB，FT⊥AB，ES⊥AB，根据平行线的判定，则ES∥PM∥FT；

根据题目中的条件：点P是EF的中点，则PE=PF；

结论：ES∥PM∥FT，PE=PF，根据平行线等分线段定理，则SM=TM，即PM是梯形EFTS的中位线；

根据梯形的中位线定理：梯形的中位线等于两底边之和的一半，则PM=(ES+FT)/2；

根据结论：AB= ES+FT，PM=(ES+FT)/2，则PM=AB/2。

总之，八年级的几何证明题是数学考试中的必考题，合理构造辅助线、灵活运用相关知识点是解决这类题型的有效办法，只有多看、多练、多总结，才能掌握解题思路和方法，为即将到来的数学期末考试助力。