初中数学几何最值终极大招，助你破解加权线段最值之谜

之前的文章对初中数学几何最值问题提供了五种解决方法，它们基本可以解决同学们遇到的最值问题。但近几年，出现了另外一种形如mAP+nAB的最值问题，运用之前的方法，根本没办法解决，难倒了绝大多数的同学，我把它归纳为加权线段之和的最值。我们先来看一下问题吧。

加权线段之和

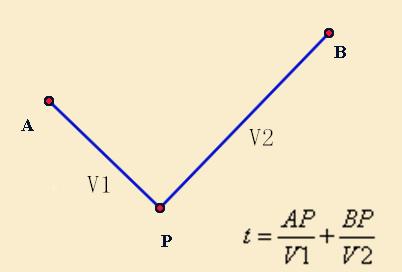
如图所示，A，B是两个定点，P点以某种轨迹运动，一个人以V1的速度走到P，然后以V2的速度走到B，求这个人所用的最短时间。这个问题乍一看，好像是将军饮马模型，但将军饮马模型只是这个问题的一个特例。当V1=V2，P点在一条直线上运动时，实际上还是求AP+PB的长度，它就是将军饮马模型，但当V1不等于V2时，即使P点还在一条直线上运动，它成了求mAP+nBP的长度，使用将军饮马模型怎么也求不出来。这个问题，因为加上了速度这一维度，使难度提高了许多，就好比牛顿经典力学遇上了相对论才能解决的问题。

在初中阶段，根据P点运动的轨迹，这个问题主要分为两类。一个是P点在一条直线上运动，对于这种问题的解决，使用的是胡不归模型。一个是P点在一个圆上运动，对于这种问题的解决，使用的是阿氏圆模型。

胡不归模型

首先，我们来看一下胡不归模型。

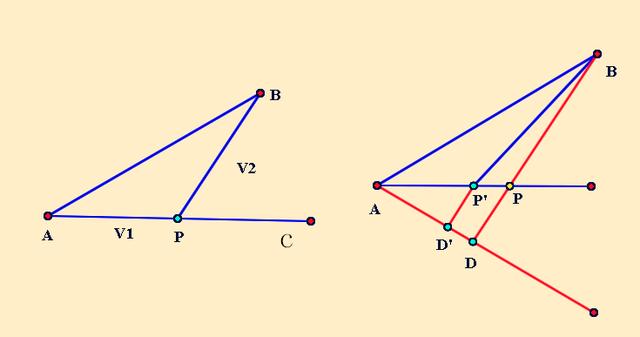
有两个定点A和B，一个动点P在AC上运动，AP段的速度是V1，PB段的速度是V2，求走完AP+BP的最短时间。它的解决思路是把两个速度作统一化处理，就是把以一个速度V1所完成的路程S1，转化成以另一个速度V2以相同速度所完成的路程S3，这样以V2速度完成的路程S3就可以和以V2速度完成的路程S3进行合并了。说的有点绕，具体到图中就很明白了，在图中，就是把V1完成的路程AP'转化成V2完成的路程P'D'，这样它们的速度一样，所以去求P'B+P'D'的最小值。根据垂线段最短，过B作垂线交于P，就是所求的点。下面我们来具体学习一下解题过程。

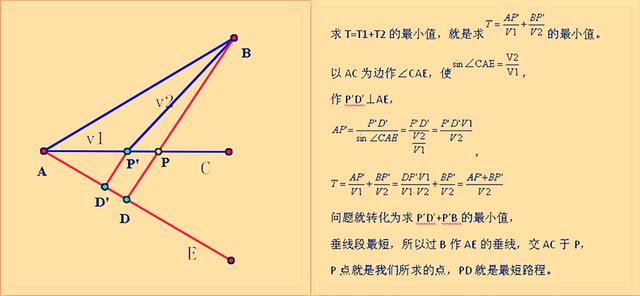
胡不归解法

以上的过程，同学们看懂了吗？可以看到，胡不归模型通常要与三角函数相结合，所以，为了方便计算，用到的数字比例，通常是特定角的三角函数值。

接下来我们来看看例题吧。

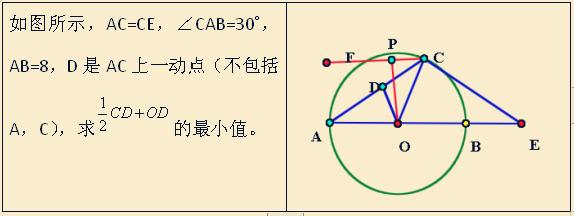
例题

我们来看看如何用胡不归模型来解这道题。当我们看到两条线段的系数不同，动点D在直线上运动，我们就要想到胡不归模型啦。同学们，你们有思路了吗？根据我们之前讲过的模型，要使用T=CD/V1+OD/V2，这道题实际上是求T=CD/2+OD/1，所以V1=2，V2=1，sin角CAO=30，我们要以AC为边再构造出一个30度的角ACF，这样，过O作CF的垂线，交CF于P，OP就是最小值。我们已经知道AB=8，那么OC=4，角OCP等于60，用三角函数，我们是不是很快就算出了结果呀。

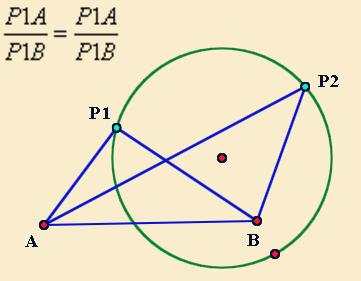
阿氏圆

第二，我们来看一下阿氏圆模型。

古希腊数学家阿波罗尼斯发现，两个定点A和B，一个动点P，当PA/PB等于一个不为1的常数时，P点的运动轨迹是一个圆。反过来就是，当P是圆上的一动点时，它到两个定点的比值相等。接下来我们看一看如何，利用这个知识解决形如mAP+nAB的最值问题。

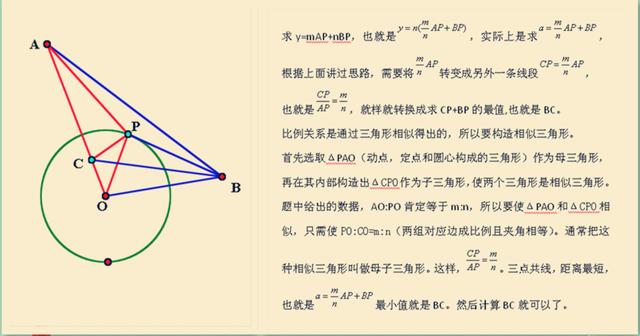
阿氏圆模型

过程有点复杂，同学们要认真看一下。关键是记住结论哈。下面我们来看一下例题吧。

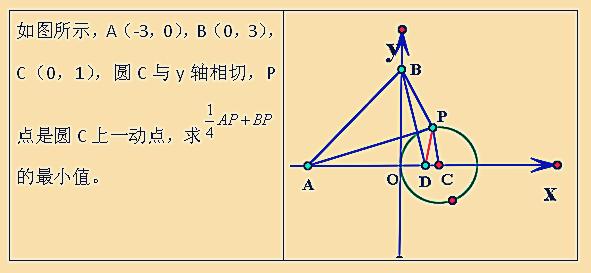
例题

大家看到A和B两个定点，P点在圆上运动，想动阿氏圆模型了吗？在这题中C是圆心，m：n=1：4，CP：AC肯定也等于1：4，我们只需要构造CD=1/4CP就可以了，连接BD，求出BD，这道题就解出来了。大家都明白了吗？

好了，胡不归模型和阿氏圆模型讲完了，我相信大家肯定有许多收获。如果考试中以填空题的形式出现，大家一定要直接应用结论，快速算出，不要浪费时间哦。