最值问题是中学阶段最重要的一块知识内容之一,一直以来都是中考热点。也是考察学生空间感,抽象思维的重要方式。
对于很多学生来说,最值问题都是缠绕着自己的噩梦,其实动点问题并不难。关键就在于把空间感树立起来。
现在总结整理了三个动态最值题型,帮助学生可以更好的,更直观的理解掌握。
一、定点到定点⇒连线段
点P在直线l上,AP+BP何时最小?
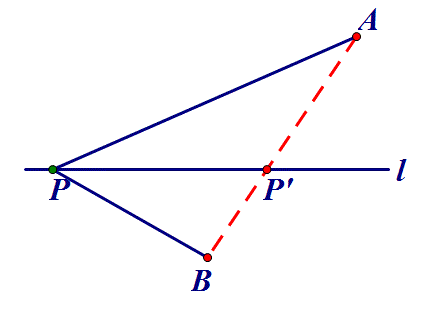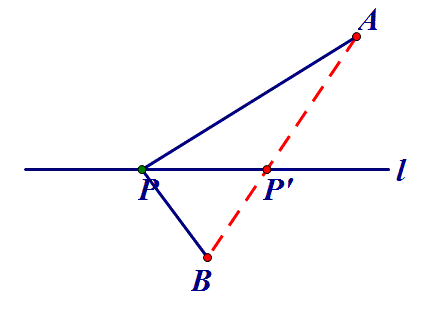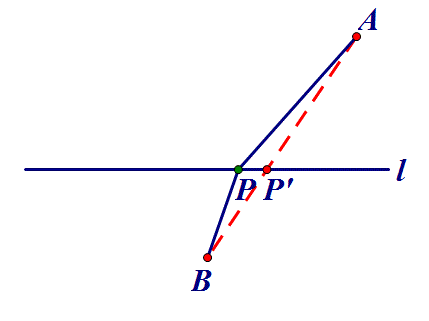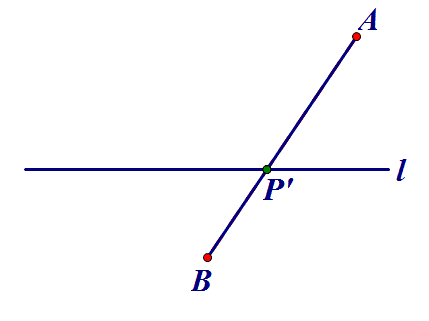
二、定点到定线⇒作垂线
点P在直线l上,AP何时最小?
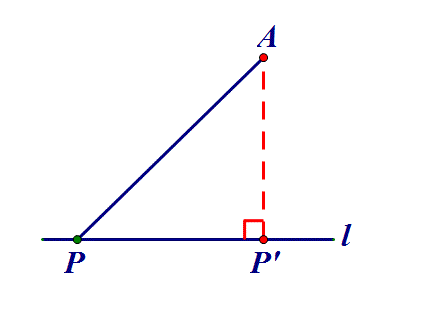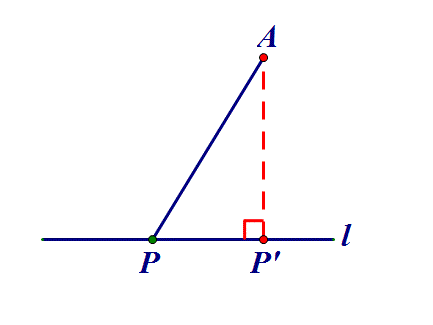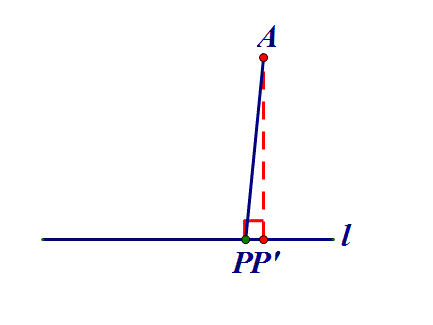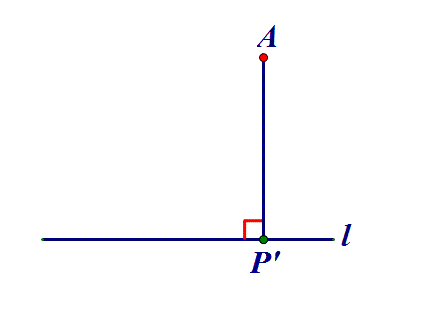
三、定点到定圆⇒连心线
点P在圆O上,AP何时最小?
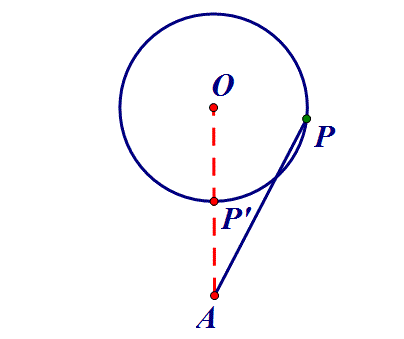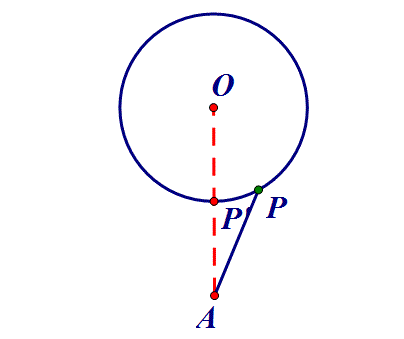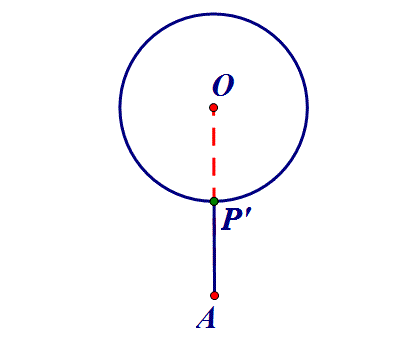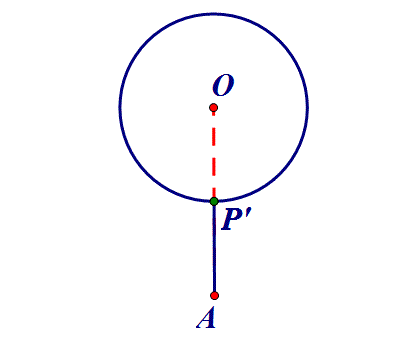
线段最值问题一般转化为上述三个问题.
例题赏析:
1.如图,∠AOB=30°,点M、N分别是射线OA、OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长最小值为 ?
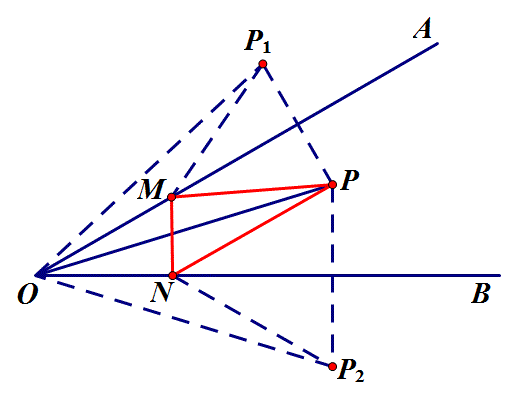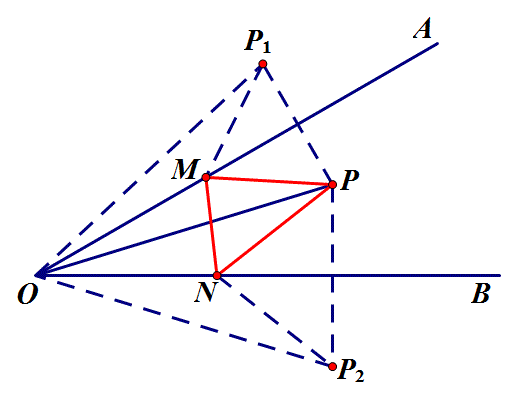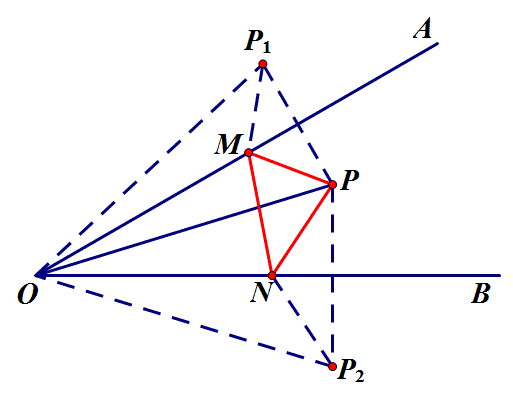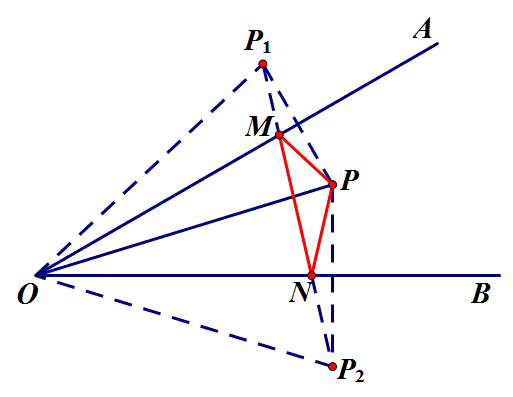
思路:把点P分别沿OA、OB翻折得P1、P2,周长即为P1M+MN+P2N,转化为求P1、P2两点之间最小值,得△PMN最小值为P1P2=OP=6.
2.如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 ?
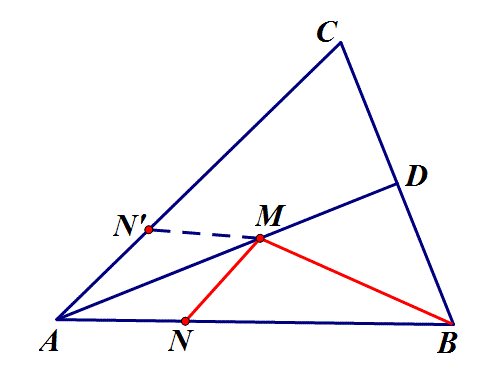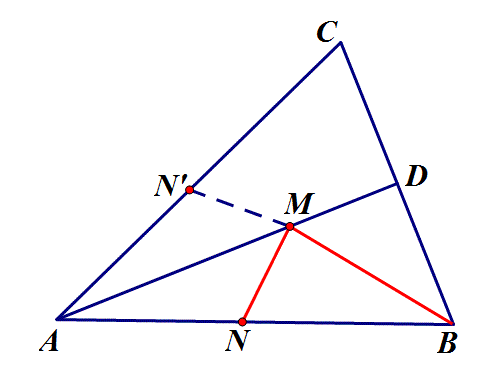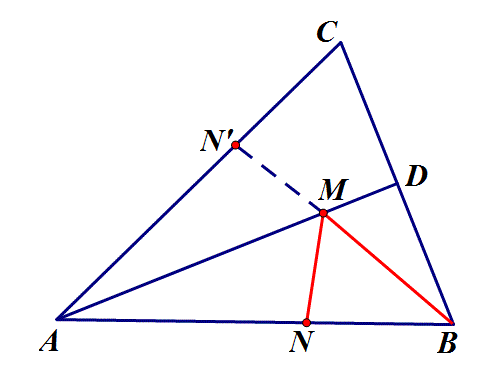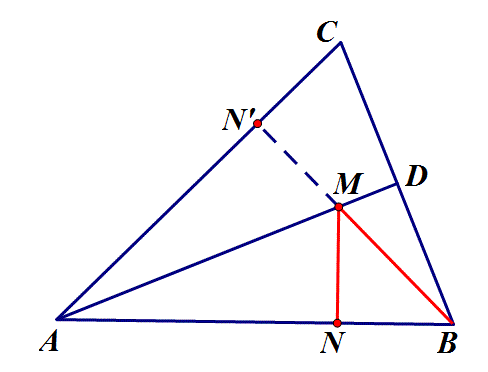
思路:点N沿AD翻折至AC上,BM+MN=BM+MN',转化为求点B到直线AC的连线最小值,即BN'⊥AC时,最小值为2√2.
3.如图,矩形ABCD中,AB=2,BC=3,以A为圆心、1为半径画圆,E是⊙A上一动点,F是BC上的一动点,则FE+FD的最小值是?
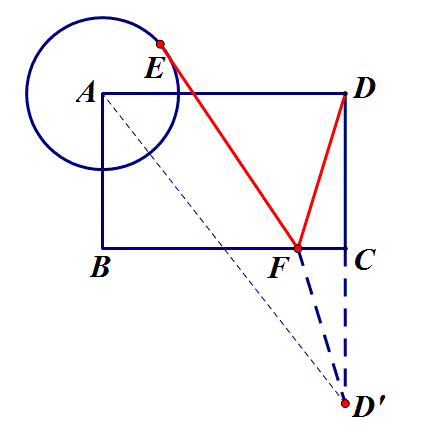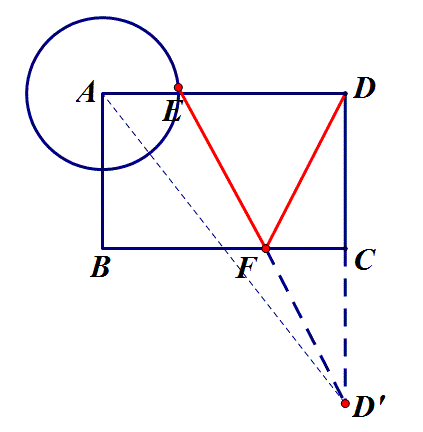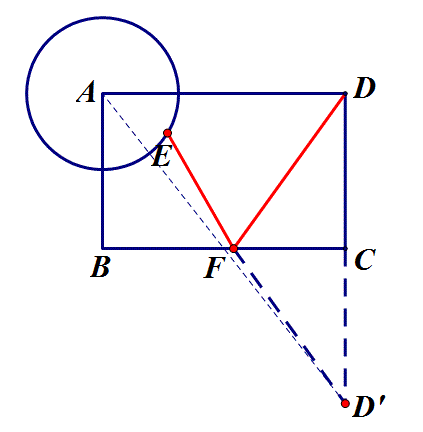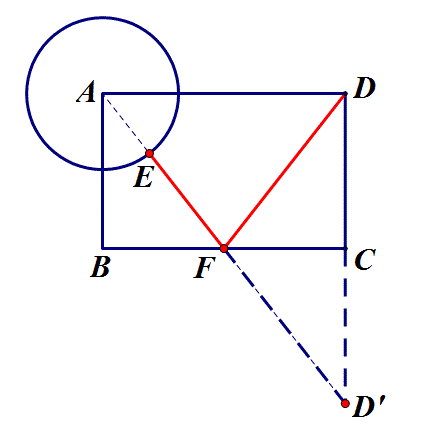
思路:点D沿BC翻折至D',DF+EF=D'F+EF,转化为求点D'到圆A上各点的最小距离,易求D'E=4.
4.在菱形ABCD中,对角线AC=8,BD=6,点E、F分别是边 AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF 的最小值,则这个最小值是 ?
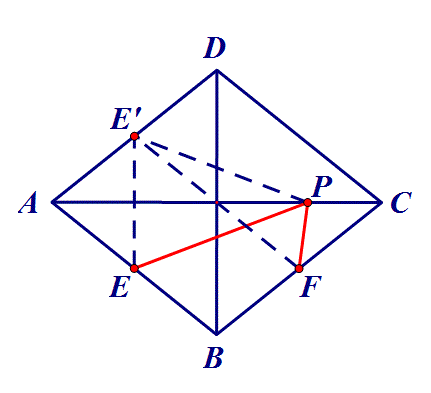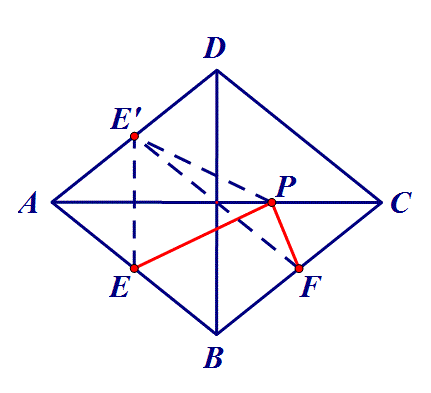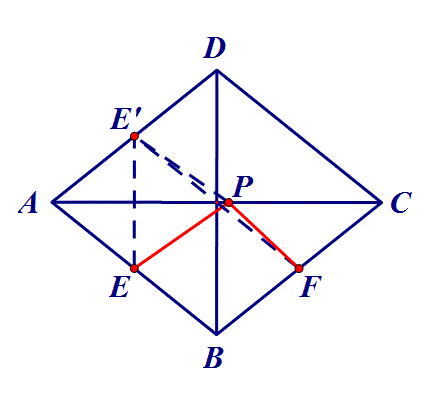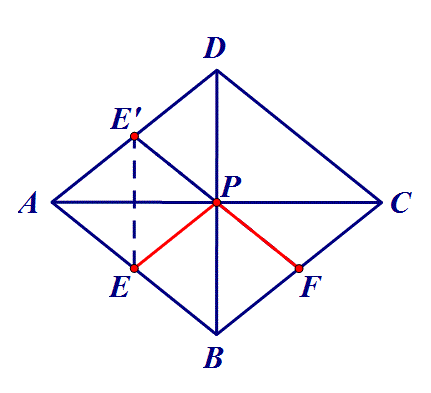
思路:点E沿AC翻折,转化为点到点的距离.(将军饮马问题实质就是通过翻折转化为定点到定点的问题)
5.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为 ?
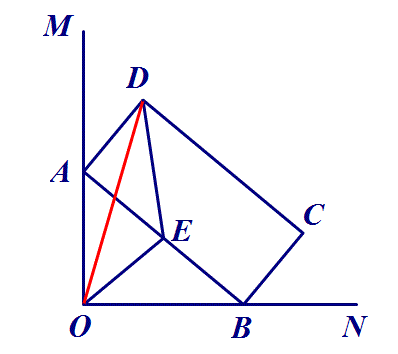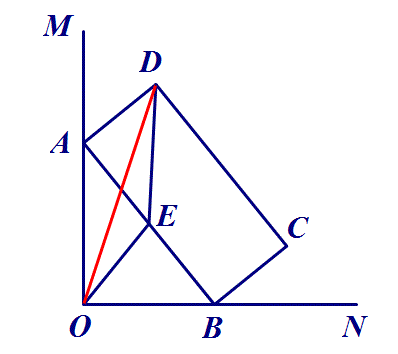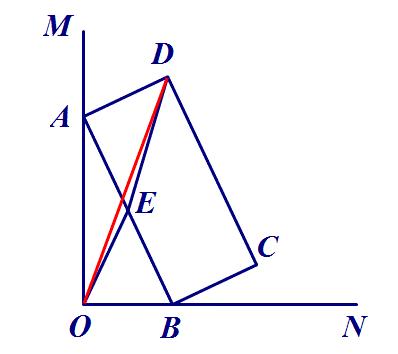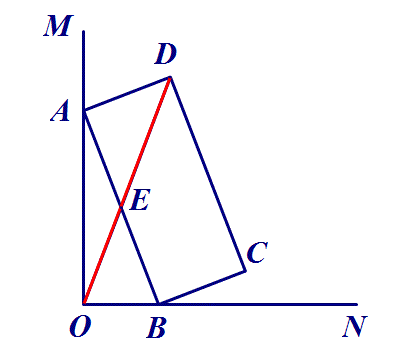
思路:取AB中点E,连接DE、OE,由两点间线段最短,得OD≤OE+DE,最大为1+√2.
6.如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是 ?
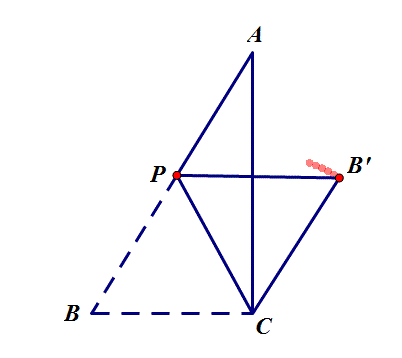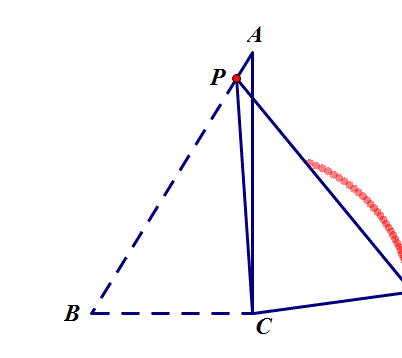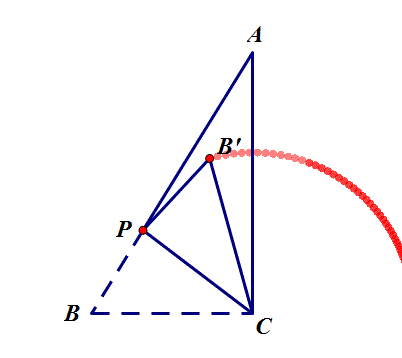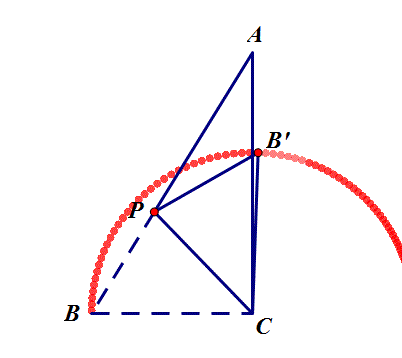
思路:B'点运动路径为以C为圆心,BC为半径的圆弧,转化为点到圆的最短距离AC-B'C=1.
7.在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是
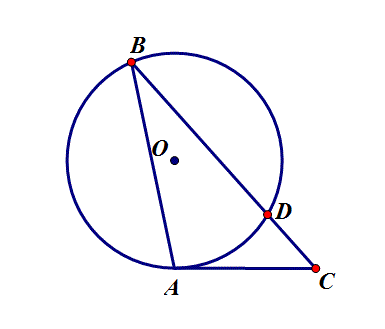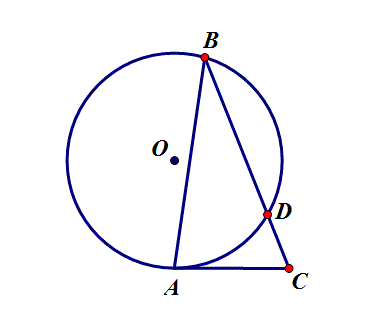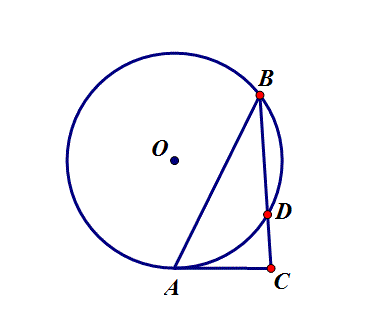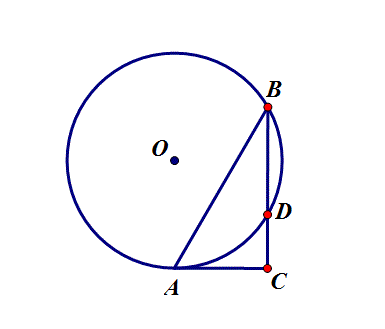
思路:D是定点,C是直线AC上的动点,转化为求点到线的最短距离.
8.在△ABC中,AB=AC=5,cos∠ABC=3/5,将△ABC绕点C顺时针旋转,得到△A'B'C,点E是BC上的中点,点F为线段AB上的动点,在△A'B'C绕点C顺时针旋转过程中,点F的对应点是F',求线段EF'长度的最大值与最小值的差.
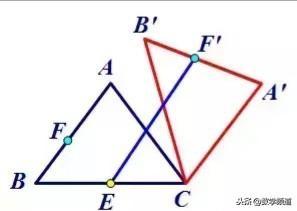
思路:先确定线段A'B'的运动轨迹是圆环,外圆半径为BC,内圆半径为AB边上的高,F'是A'B'上任意一点,因此F'的运动轨迹是圆环内的任意一点,由此转化为点E到圆环的最短和最长距离.
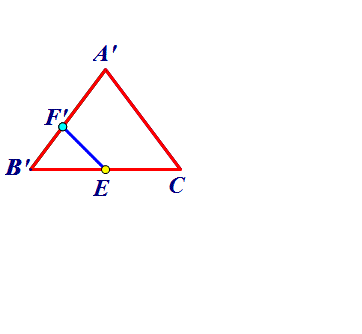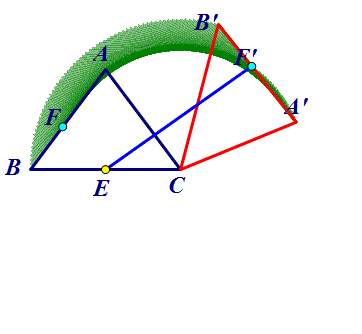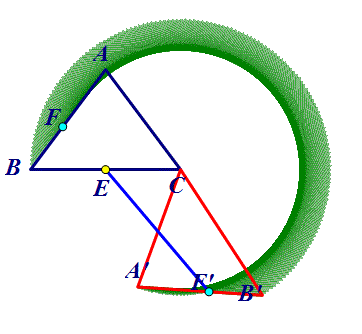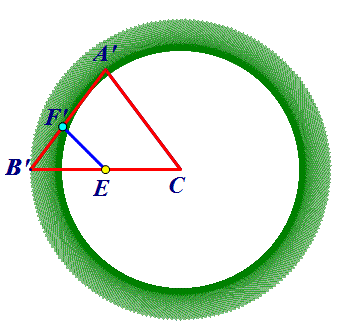
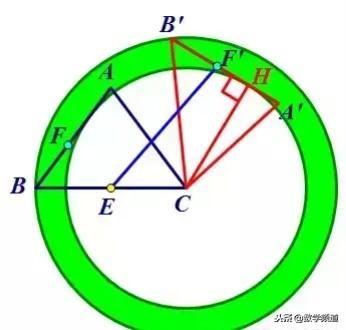
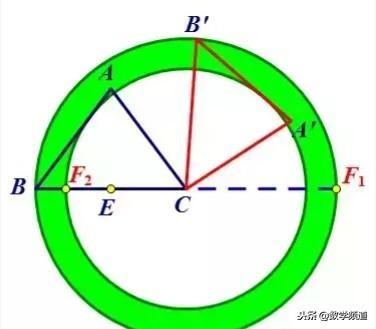
E到圆环的最短距离为EF2=CF2-CE=4.8-3=1.8,E到圆环的最长距离为EF1=EC+CF1=3+6=9,其差为7.2.
问:何时需要作辅助线翻折其中的定点(定线或定圆)?
答:当动点所在直线不在定点(定线或定圆)之间时,需把定点(定线或定圆)沿动点所在直线翻折以使定点(定线或定圆)处于动点所在直线的两侧,从而便于连接相关线段或作垂线与动点所在直线找到交点.如上述例3,动点F所在直线不在定圆A和定点D之间,因而需把D点沿BC翻折至D',即可转化为定点D'到定圆A的最短距离,另外亦可把圆A沿BC翻折至另一侧,同样可以转化为定点D到定圆A'的最短距离,如下图.
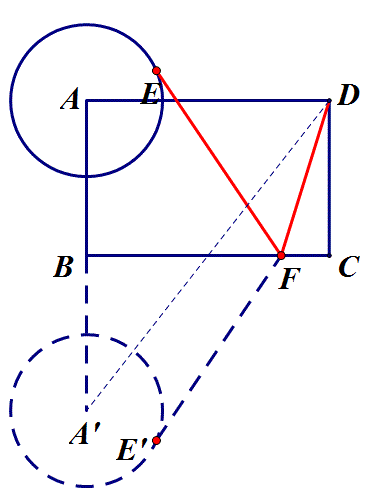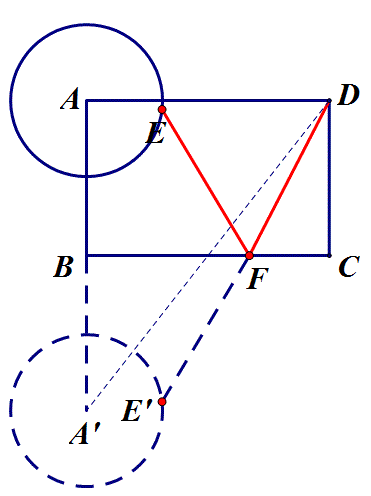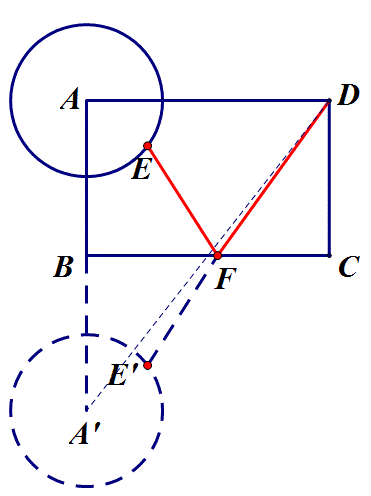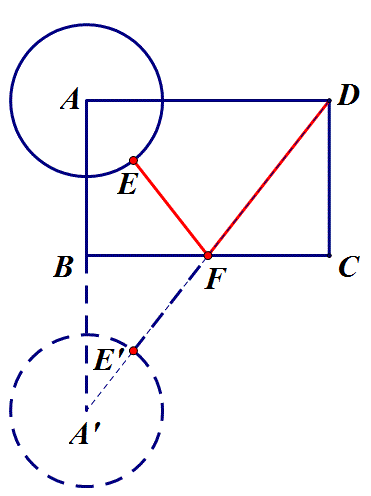
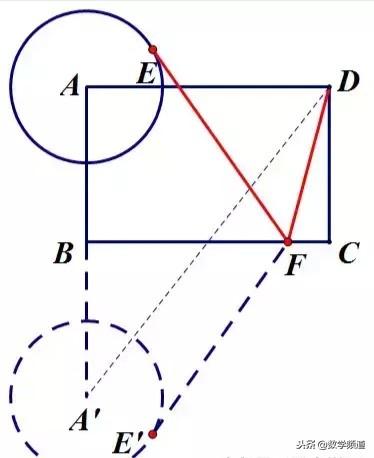
关键方法:动中求定,动点化定线;以定制动,定点翻两边.
(1)动中求定,动点化定线:如例7、例8、例10,动点所在路径未画出时需先画出动点所在轨迹,一般动点所在轨迹为线或圆.
(2)以定制动,定点翻两边:如例1、例2、例3、例5,定点(线或圆)在动点所在直线同侧时需翻折至两侧,转化为上述三种关系.

 加载中,请稍侯......
加载中,请稍侯......
精彩评论