勾股定理应用中蕴含的数学思想

勾股定理是初中数学中的一个重要应理，它是沟通几何与代数的桥梁，也是反映自然界基本规律的一条结论.在运用勾股定理解题时，若能正确把握数学思想，则会开阔解题思路，优化解题过程，同时也能加深对数学概念、公式、定理的理解.下面举例说明勾股定理应用中蕴含的数学思想，以作参考.

一、方程思想

方程思想是指运用适当的数学语言，从问题的数量关系出发，通过设未知数，将问题中的条件转化为数学模型——方程(组)，然后运用相应的知识来求解问题的一种数学思想.

例1 如图1，矩形ABCD中，BC=3，且BC>AB，E为AB边上任意一点(不与A,B重合).设BE=t，将⊿BCE沿CE对折，得到⊿FCE，延长EF交CD的延长线于点G，则tan∠CGE= .(用含t的代数式表示)

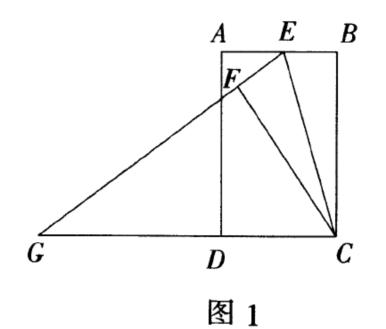
评注：本题主要考查矩形的性质，轴对称变换的性质，正切的定义及勾股定理.其中，运用勾股定理构建方程，把已知量与未知量建立关系是解题的关键;同时也体现了运用方程思想解题的简便快捷.

二、转化思想

转化思想又叫化归思想，就是指将需要解决的问题由难化易，由繁化简，从而实现化未知为已知的数学思想.

例2 将两块三角板如图2放置.其中∠C=∠EDB=90°，∠A=45°，∠E=30°，AB=DE=6，求重叠部分四边形DBCF的面积.

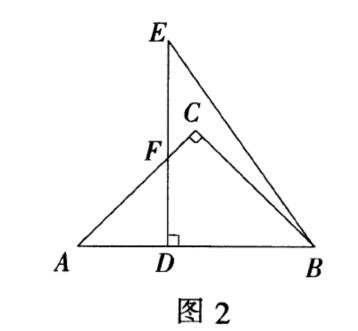
评注：本题中四边形DBCF的面积很难直接求得，将其转化为⊿ABC与⊿ADF的面积差是解决问题的关键.由此可见，转化策略是数学解题中一种常用的思想方法，可以说，数学解题的过程实际就是问题转化的过程.

三、数形结合思想

数形结合思想就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过抽象思维与形象思维的结合，使复杂问题简单化，抽象问题具体化的一种数学思想.

评注：本题结合勾股定理，通过构造几何图形，再利用图形中边与边的关系求出了最小值，充分体现了数形结合思想的优越性.其实勾股定理本身就是数形结合的定理，它的验证和应用都体现了数形结合的思想.

四、分类讨论思想

分类讨论思想是指，当一个数学问题所给的对象不能进行统一研究，就需要对研究对象按某个标准分类，然后对每一类分别研究，得出每一类结论，最后综合各类结果得到整个问题解答的数学思想.

例4 在⊿ABC中，BC=a,AC=b,AB=c，若∠C=90°，如图4，根据勾股定理，则a²+b²=c²

.若⊿ABC不是直角三角形，如图5和图6，请你类比勾股定理，试猜想a²+b²与c²的关系，并证明你的结论.

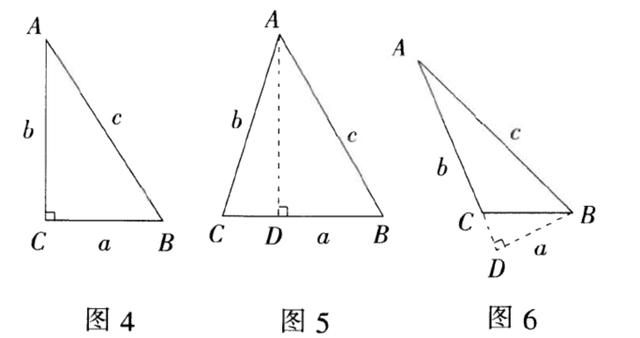
评注:本题通过类比勾股定理，分两种情况对a²+b²与c²的大小关系作出判断，体现了分类讨论的解题思想.数学里的许多问题，在解答过程中只有用分类讨论的思想，才能保证解答完整准确，做到“不漏不重”.

五、整体代换思想

整体思想就是指在研究和解决数学问题时，通过研究问题的整体形式、整体结构、整体特征，从整体上认识问题、思考问题，从而对问题进行整体处理的思想方法.

例5 如图7，在RT⊿ABC中，∠BAC=90°，M,N是斜边BC的三等分点，已知AM=4,AN=3，则BC= .

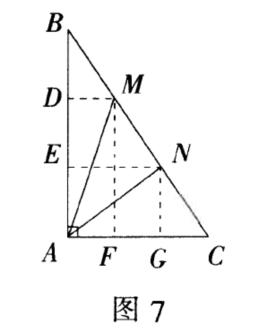
评注:本题中AC和AB的长无法直接求出，于是把AC²+AB²看作一个整体进行求值，其它问题便迎刃而解.可以看出，运用整体思想解题能使复杂问题简单化，难度大大降低，起到一举解决问题的作用.

总之，数学思想方法是随着学生对数学知识的学习、运用逐渐形成的，它是数学的生命和灵魂，是数学知识的精髓，是把知识转化为能力的桥梁，同时也是对数学内容的一种本质认识.在运用勾股定理解决问题的过程中，如果能抓住思想方法，就抓住了问题的本质.