勾股定理：几何最短路径问题

最短路线问题通常是以“平面内连结两点的线中，线段最短”为原则引申出来的.人们在生产、生活实践中，常常遇到带有某种限制条件的最近路线即最短路线问题.

对于数学中的最短路线问题可以分为两大类：第一类为在同一平面内；第二类为空间几何体中的最短路线问题，对于平面内的最短路线问题可先画出方案图，然后确定最短距离及路径图。对于几何题内问题的关键是将立体图形转化为平面问题求解，然后构造直角三角形，利用勾股定理求解.

方法总结：①解决立体图形中最短距离问题的关键是把立体图形平面化，即把立体图形沿着某一条线展开，转化为平面问题后，借助“两点之间，线段最短”或“垂线段最短”，进而构造直角三角形，借助勾股定理求解.

②平面图形的最短路径通常是作轴对称变换，转化为“两点之间线段最短”的模型来解决问题.

常见的有圆柱体的展开、长方体的展开、楼梯的展开、绕绳的展开等等，下面我们就通过一些典型的例题对这些问题逐一讲解.

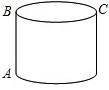
例题1：如图有一圆柱体如图，高8cm，底面半径5cm，A处有一蚂蚁，若蚂蚁欲爬行到C处，求蚂蚁爬行的最短距离________.（π取3）

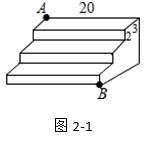
例题2：如图是一个三级台阶，它的每一级的长宽和高分别为20、3、2，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是_______．

【点睛】本题用到台阶的平面展开图，只要根据题意判断出长方形的长和宽，并借助勾股定理即可解答．

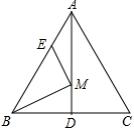
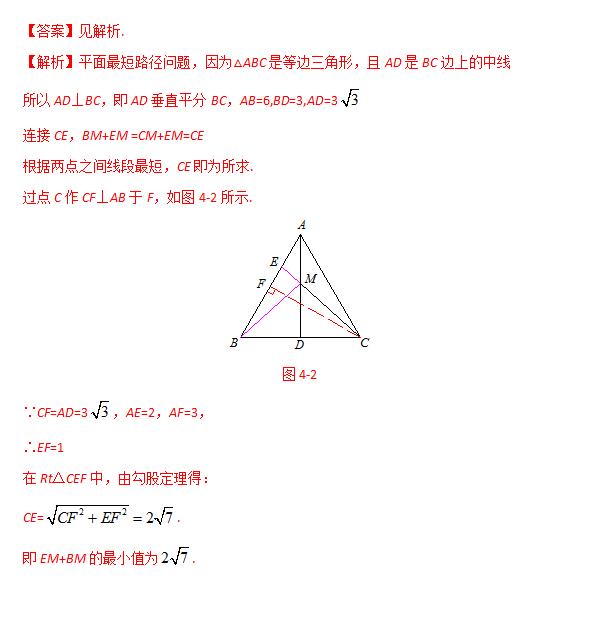
例题3：如图等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是AB边上一点，若AE=2，求EM+BM的最小值．

例题4：如图一只蚂蚁沿着图示的路线从圆柱高AA1的端点A到达A1，若圆柱底面半径为6/π，高为5，则蚂蚁爬行的最短距离为__________.

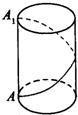
【答案】13.

【解析】因为圆柱底面圆的周长为2π×6/π=12，高为5，

所以将侧面展开为一长为12，宽为5的矩形，

根据勾股定理，求得展开后矩形的对角线长为13．

即蚂蚁爬行的最短距离为13．

故答案为：13.

例题5：如图在△ABC中，∠C=90°，∠BAC=30°，AB=，AD平分∠BAC，点P、Q分别是AB、AD边上的动点，则PQ+BQ的最小值是 ________.