基本图形分析法：详细分析直角三角形斜边的中线问题（四）

【分析方法导引】

当几何问题中出现了直角三角形斜边上的中点时，就应想到要应用直角三角形斜边上的中线的基本图形的性质进行证明。接下来就应将斜边上的中线添上。进一步的分析就是：若斜边上的中点是条件，则直接推得斜边上的中线等于斜边的一半，并可直接应用两等腰三角形推得角之间的等量关系。若斜边上的中点是要证明的结论，则应转而证明要证相等的这两条线段都和这条斜边上的中线相等，也就是转化为等腰三角形的判定问题或者也就是证明角相等的问题。进一步也就是应用线段相等与角相等之间的等价关系来完成分析。

当几何问题中出现了线段之间的倍半关系，且倍线段是直角三角形的斜边时，就应想到要应用直角三角形斜边上的基本图形进行证明。接下来就应将斜边上的中线添上，得到这条斜边上的中线等于斜边的一半，和相应的角之间的等量关系和倍半关系，问题就转化成要证明问题中出现的倍半关系中的半线段与这条斜边上的中线相等。

当几何问题中出现了两个角之间的倍半关系，且其中的半角是一个直角三角形的锐角时，就可想到要应用直角三角形斜边上的中线的基本图形进行证明。接下来的问题也是将斜边上的中线添上，然后可应用两个等腰三角形的顶角的外角等于底角的两倍的性质来完成分析。

例7 如图3-214，已知：△ABC中，∠C=90°，D是AB的中点，E是AC上的一点，且CE=BD，ED的延长线交CB的延长线于F。求证:∠F=1/2·∠A。

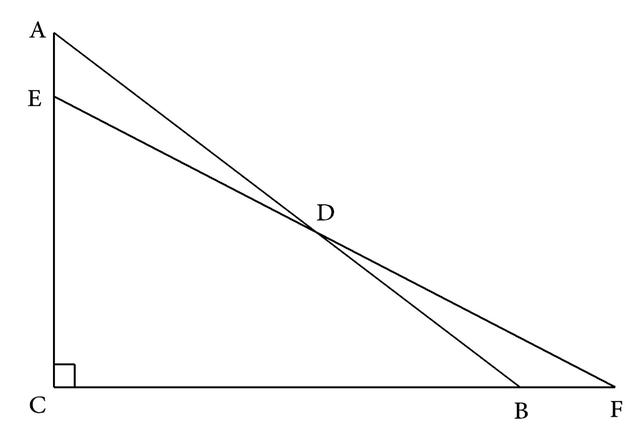
图3-214

分析:本题的条件中出现了∠C=90°和D是斜边AB的中点，所以可应用直角三角形斜边上的中线的基本图形进行证明。由于图形中只有直角三角形而没有斜边上的中线，所以应将斜边上的中线添上，也就是连结CD(如图3-215)，即可得CD=AD= BD，∠A=∠DCA，这样问题就成为应证∠F=1/2·∠DCA。

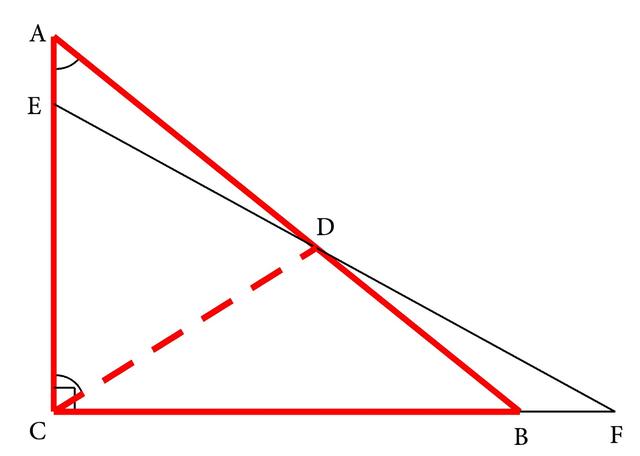
图3-215

由条件CE=BD，又可得CE=CD，这是两条具有公共端点C的相等线段，它们就可以组成一个等腰三角形，而要证明的性质中的倍角，即∠DCA就是这个等腰三角形的顶角。

现在我们要证明的性质是两个角之间的倍半关系，所以可根据角的倍半关系的定义，将大的角两等分，也就是作∠DCA的角平分线并交DE于G后(如图3-216)，证明它的一半，亦即∠ECG和∠F相等。由于我们作的是等腰三角形顶角的角平分线，所以可应用等腰三角形中重要线段的基本图形的性质得CG⊥DE， 而已知∠ECF=90°，这样CG就成为直角△EFC的斜边上的高，于是应用直角三角形斜边上的高的基本图形的性质就能推得∠ECG=∠F。

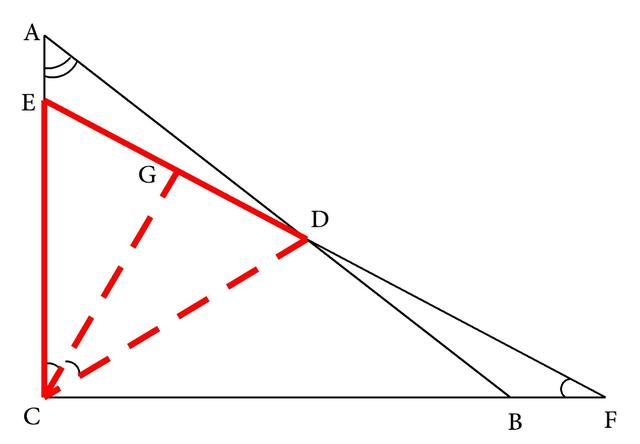
图3-216

在证明两个角的倍关系时，也可以根据角的倍半关系的定义，作出小的角的两倍，再证明所作出的角与大的角相等，于是以FC为边，F为顶点作∠CFG=∠CFE，且交AC的延长线于G(如图3-217)，问题就成为要证∠EFG=∠DCE。由于作出FG后CF就是∠EFG的角平分线，且EG⊥FC，出现了角平分线和向角平分线所作垂线之间的组合关系，从而可得到△FEG是等腰三角形，亦即FE=FG，而我们已证△CDE也是等腰三角形，CE=CD，且这两个等腰三角形有一个公共的底角，即∠DEC，所以它们的顶角必定相等，分析也就可以完成。

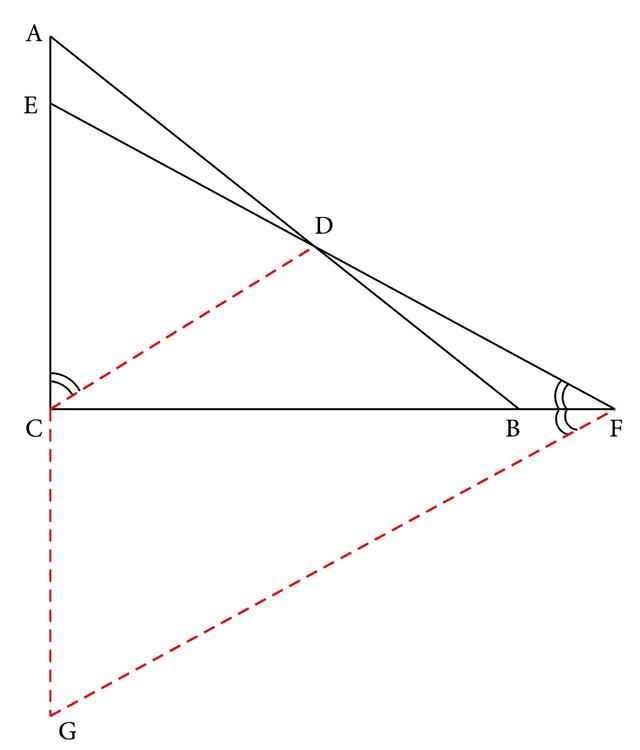
图3-217

例8 如图3-218，已知：D是半圆O的直径AB上的一点，AC是弦，过D作AB的垂线交AC于E，交BC的延长线于F，过C作半圆的切线交EF于G。求证:EG=FG。

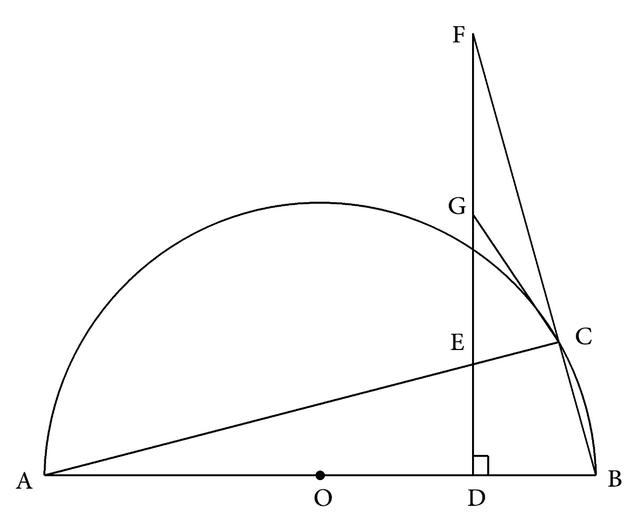
图3-218

分析:本题条件中出现AB是半圆的直径，C是半圆上的一点，所以可应用半圆上的圆周角的基本图形的性质进行证明，于是可得∠ACB=90°，又因为B、C、F成一直线，所以∠ECF也等于90°。

本题要证的结论是EG=FG，这样就出现了G应是直角△FEC的斜边的中点，从而就可应用直角三角形斜边上的中线的基本图形的性质进行证明(如图3-219)，也就是要证明EG= FG，就应证明EG和FG都和CG相等，进一步也就是转化为要证明EG=FG的等价性质∠GCE=∠GEC。

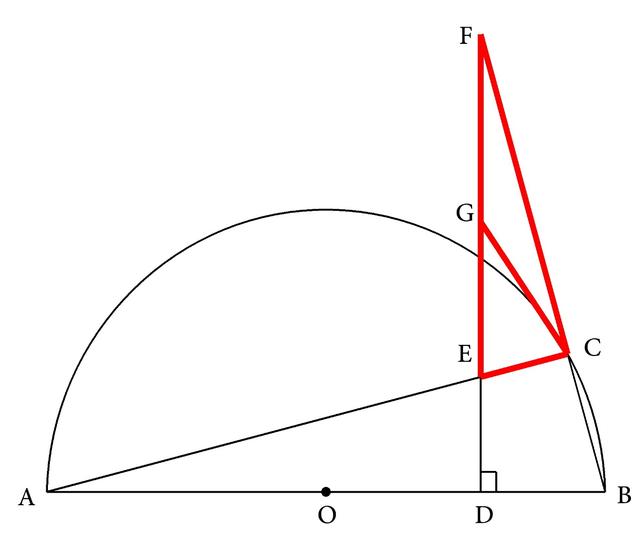
图3-219

由条件GC与半圆相切于C，CA是过切点的弦，所以可应用弦切角的基本图形的性质进行证明，也就可得∠GCA=∠B，这样问题就成为要证∠GEC也等于∠B。从图形上我们可以看出∠GEC是四边形EDBC的一个外角，因此要证∠GEC=∠B，就应证E、D、B、 C四点共圆，而已知∠EDB=90°，已证明∠ECB=90°，所以E、D、B、C四点共圆可以证明。

在得到了∠GCE=∠GEC后，即可推得EG=CG，而由∠ECF=90°，又可推得∠GCF=∠F，又可得FG=CG，分析就可以完成。