一·函数的切线

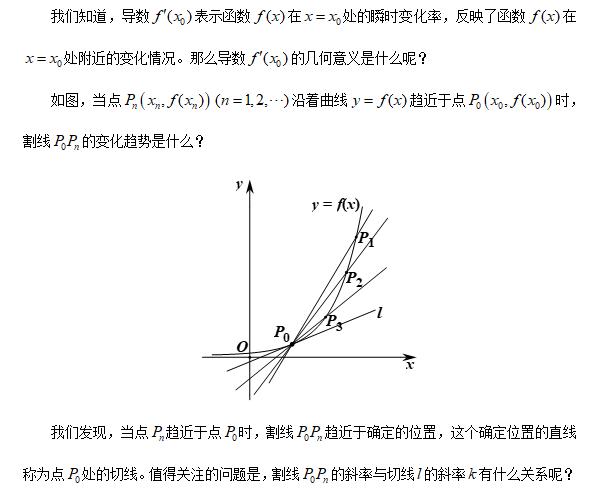
二·导数的几何意义

数学上常用简单的对象刻画复杂的对象，这里我们用曲线上某点处的切线来近似代替这一点处附近的曲线，这是微积分中重要的思想方法——以直代曲。

三·高考题型归纳

高考中，关于导数的几何意义问题，主要以选择题或填空题形式出现，难度主要以中低档题出现，偶尔也会有较难试题，此时导数的几何意义仅仅作为中间步骤而已。

导数的几何意义常考题型包括：（1）直接求切线的斜率；（2）求切线方程或者法线方程；（3）求切点的坐标；（4）求参数的值；（5）曲线的公切线问题；（6）与其他知识相关的综合性问题。

1·求切线的斜率：

2·求切线方程：

3·去参数的值：

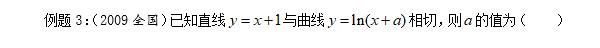
4·求切点坐标：

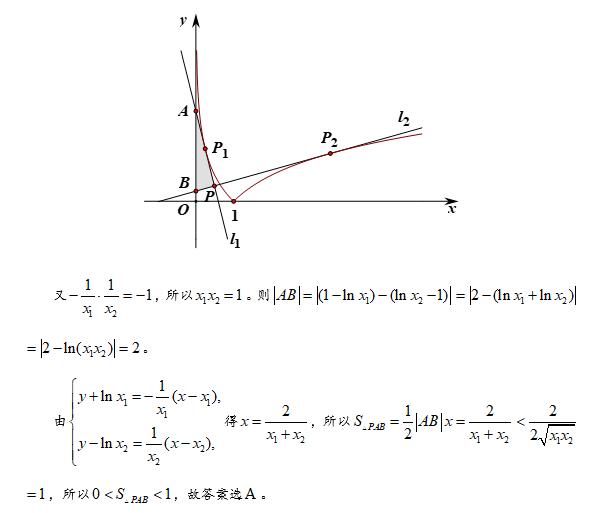
5·公切线问题：

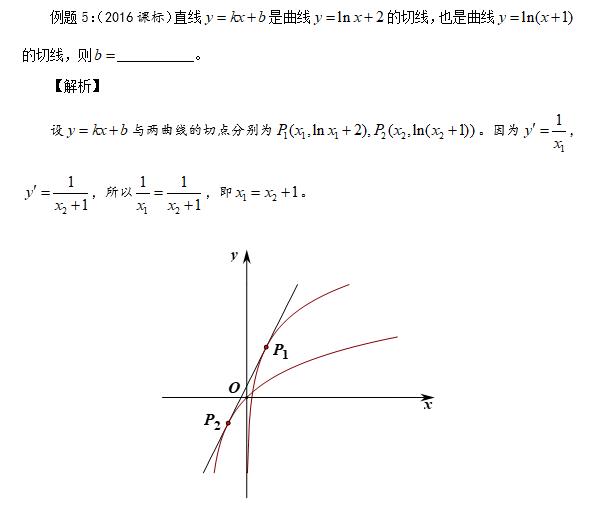
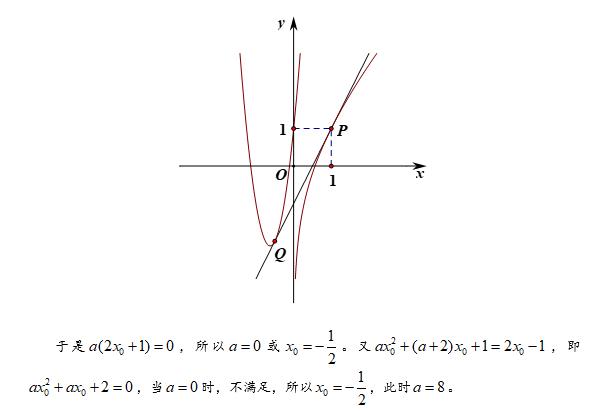
6.综合问题：