勾股定理与最短路径问题
最短路径问题的核心理论是:两点之间线段最短,但在不同情形中,会以不同的方式出现,也就会涉及到不同的思路和方法,比如在【几何模型】“将军饮马”问题——作一首小诗这一讲中,主要利用到"两点之间线段最短"和"三角形两边之和大于第三边"(三角形的三边关系本质上还是"两点之间线段最短"),而这一讲,我们主要涉及到立体图形的最短路径问题。
一、立体图形的最短路径问题的解决思路
对于立体图形的最短路径问题,我们一般是利用"横切"或"展开"等手段,将其转换到平面图形中解决,而这种情形不免会在直角三角形中解决,也自然会和勾股定理扯上关系
二、利用"横切",转换成平面图形
【例】
如图,有一个透明的直圆柱状的玻璃杯,现测得内径为5cm,高为12cm,今有一只14cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度最少为多少?
(注:内径即底面直径)
【分析】
若使吸管露出杯口最短,自然留在杯中最长,而最长莫过于下列情况:
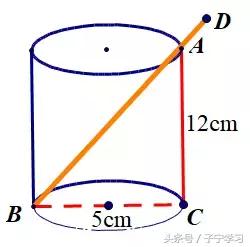
这样,按照上图将圆柱"横切",就可以将其转换到RT△ACB中解决,而AB可有勾股定理解得:AB=13cm,所以吸管露出杯口的最短长度AD=BD-AB=1cm
【练习题】
如图,将一根25cm长的细木棒,放入长、宽、高分别为8cm、6cm、10cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是多少?(保留1位小数)。

三、利用"展开",转换成平面图形
这类问题又可以细分为两种情形:直面(正方体或长方体)和曲面(圆柱),但无论直面或曲面,一般都是展开为矩形,进而利用勾股定理解决
【例】直面(正方体或长方体)
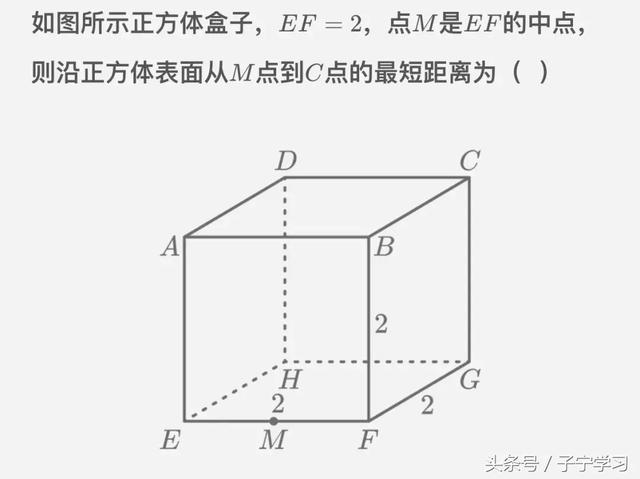
【分析】
研究在表面从点M到点C的最短路径,可以将正方体表面局部展开:
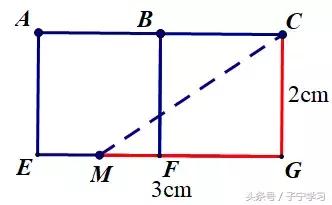
根据“两点之间线段最短",可知最短路径,即为线段MC。进而,在RT△CGM中,利用勾股定理,可求MC
【练习题】
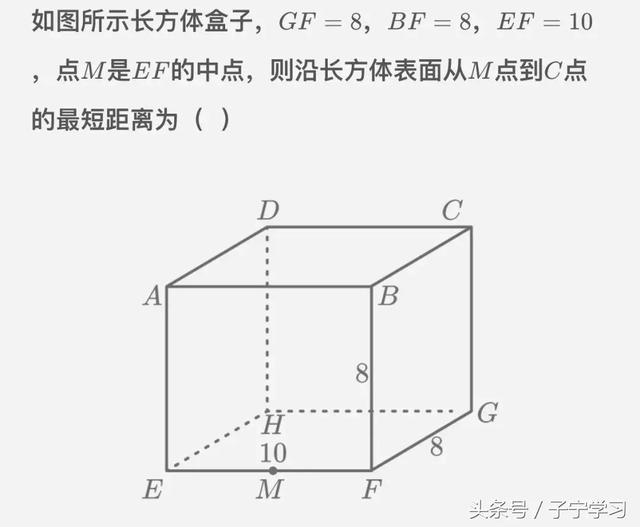
【例】曲面(圆柱)如图,圆柱高15cm,底面半径为8/兀cm,一蚂蚁从B点爬到A点的最短路径为多少?
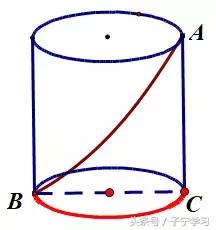

【分析】
请注意:此题的易错点是,很多同学直接连接AB,认为此时线段AB即为最短路径。拜托,你的蚂蚁会"穿墙术"吗?
这里是从圆柱表面爬行,即在曲面上爬行。也就是说,在"视觉上",蚂蚁是按照"曲线"爬行的(实际上,还是一条直线)

尽管如此,我们仍然可以把这个圆柱表面局部展开,可得:
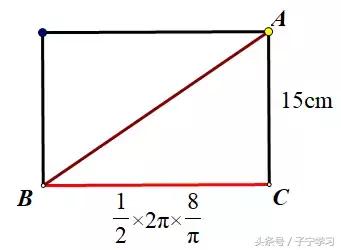
关键点:这里的线段BC长,实际上是指上图中,半圆BC的长度(红色部分)
根据"两点之间线段最短",可知最短路径,即为线段AB。进而,在RT△ACB中,利用勾股定理,可求最短路径AB长
【练习题】
如图,以A点环绕油罐建梯子,使它正好落在A点的正上方B点处,问梯子最短要多少米?(已知油罐底面半径为6/π m,AB为5m)

 加载中,请稍侯......
加载中,请稍侯......
精彩评论