基本图形分析法：“三步曲”式分析初中几何中的弦切角难题

什么是基本图形分析法？

它的目的在于剖析、介绍和论述对几何问题的思维过程、分析过程。所以也就成为思考和解决几何问题的工具和路灯。

面对初中经典几何题，基本图形分析法会告诉你：

1） 拿到问题后是怎么想的？

2） 是怎么一步一步想出来的？

3） 为什么要这样想？

这样一套几何分析"三步曲"，难题也就迎刃而解了。今天依然延续之前的含有弦切角的几何例题，欢迎大家多挑毛病，多提意见。也欢迎大家关注我们，获取更多基本图形分析法文章。

例63如图4-172，已知：⊙O与⊙O′外切于C，OO′的延长线交⊙O、⊙O′于A、B，过C作CD⊥AB交以AB为直径的半圆于D，AD、BD分别交⊙O、⊙O′于E、F。求证：EF是⊙O、⊙O′的外公切线。

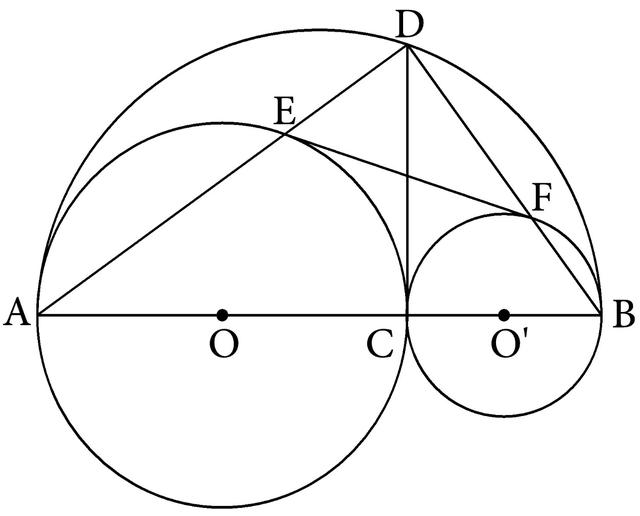
图4-172

分析：本题要证明EF是⊙O、⊙O′的外公切线，所以可根据两圆的外公切线的定义，证明EF分别与两个圆相切。

由条件AC、BC分别是⊙O、⊙O′的直径，所以可应用半圆上的圆周角的基本图形的性质来进行证明。现在图形中是有直径，有半圆上的点E、F，而没有圆周角，所以应将圆周角添上，于是联结CE、CF（如图4-173），可得∠AEC=∠CFB=90°

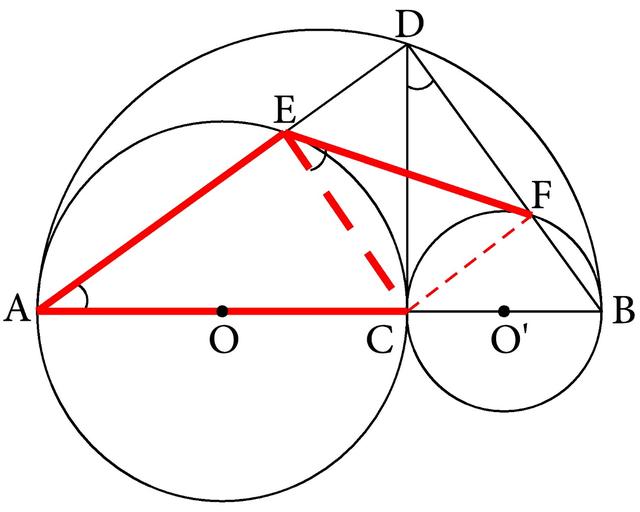
图4-173

现在的问题是要证FE与⊙O相切于E，所以就可应用弦切角的基本图形的性质进行证明，由于EC应是过切点的弦，所以问题就成为要证明∠FEC=∠A。

而由我们已得的∠CEA=∠CFB=90°，以及A、E、D和B、F、D都成一直线，又可得∠CED=∠CFD=90°，D、E、C、F四点共圆，所以∠FEC=∠FDC，于是问题就转化为要证∠FDC=∠A

再由条件AB是半圆的直径，D是半圆上的一点，所以∠ADB=90°，而条件中还给出CD⊥AB，这样CD就成为直角△ABD的斜边上的高，于是应用直角三角形斜边上高的基本图形的性质可得∠BDC=∠A。根据同样的道理，也可以证明FE与⊙O′相切于F，分析即可完成。

本题要证明FE与⊙O相切于E，所以也可以直接根据切线的判定定理，联结OE（如图4-174）后，应证∠FEO=90°，而已知A、E、D成一直线，从而也就是要证∠AEO+∠DEF=90°

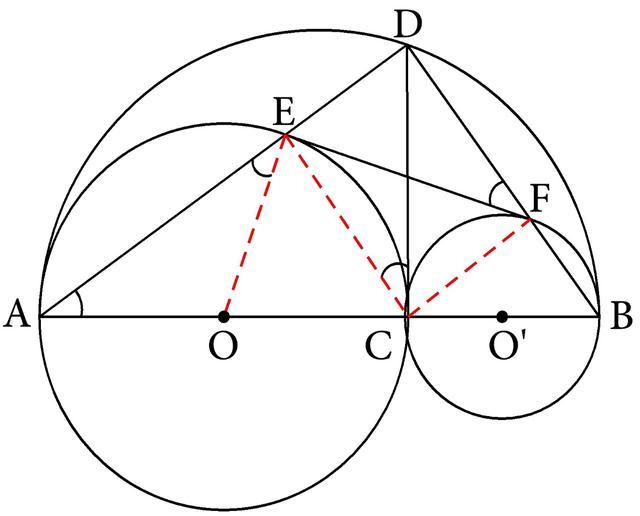
图4-174

由条件AB是半圆的直径，D是半圆上的一点，所以有∠ADB=90°，那么在△FED中，就有∠DFE+∠DEF=90°，问题也就转化成要证∠AEO=∠DFE。

由条件OE和OA都是⊙O的半径，它们可组成等腰三角形，从而就可由OA=OE，推得∠AEO=∠A。

又因为条件中给出CD⊥AB，且由AC是⊙O的直径，E是半圆上的一点，所以联结CE后（如图4-174），可得∠AEC=90°，从而又出现了CE是直角△ADC的斜边上的高，那么又可以应用直角三角形斜边上的高的基本图形的性质，得∠A=∠DCE。

再由BC是⊙O′的直径，F是半圆上的一点，所以联结CF后（如图4-174），有∠BFC=90°，那么由A、E、D和B、F、D都成一直线，可得∠CED=∠CFD=90°，C、F、D、E四点共圆，∠DCE=∠DFE。所以∠AEO=∠DFE就可以证明。