基本图形分析法：如何运用轴对称型图形得到求证对应线段

当几何问题里要求证线段关系时，首先就应通过观察图形，并根据已知的条件，将求证的线段关系转换为等价的对应线段。今天的这道经典例题就利用两种辅助线的方式，分别得到轴对称图形，进而得到线段对应关系。

例8 如图5-18，已知：△ABC中，AB=AC，∠A=100°，CD是角平分线。求证：BC=CD+AD

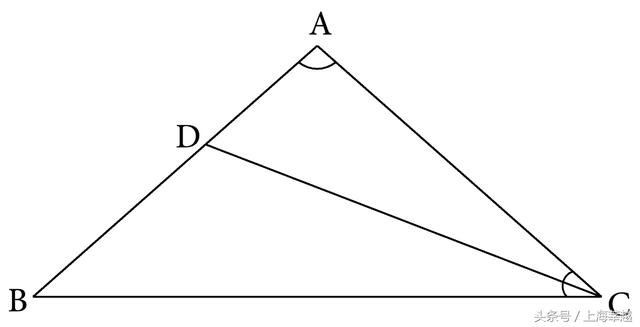
图5-18

分析：本题要证的结论BC=CD+AD，是一条线段等于两条线段的和，所以可根据线段和差关系的定义，在线段CB上截取CE=CD（如图5-19），然后应证BE=AD。由于截得的线段CE和CD是两条具有公共端点的相等线段，所以它们可组成一个等腰三角形，现在这个等腰三角形只有两条腰而没有底边，所以联结DE（如图5-19），就可得∠CDE=∠CED。

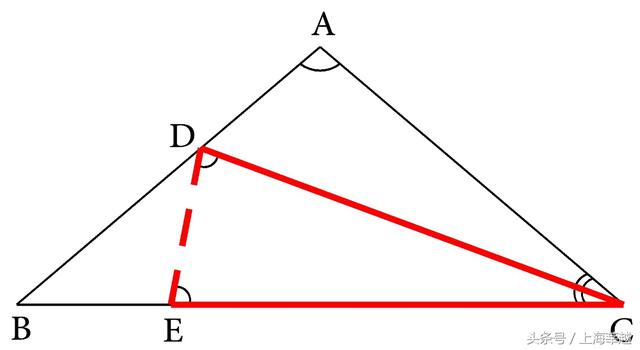
图5-19

由条件AB=AC，∠A=100°，应用等腰三角形的性质可得∠B=∠ACB=1/2·(180°-100°)=40°，而CD是角平分线，所以∠BCD=1/2·40°=20°，于是就有∠CED=1/2·(180°-20°)=80°，从而就得到∠CED=2∠B，而由B、E、C成一直线，又有∠CED是△EBD的外角，由此就得△EBD是等腰三角形或BE=DE，这样问题就成为应证DE=AD。

由于条件中给出CD是角平分线，所以∠BCD和∠ACD这两个相等的角就是关于CD成轴对称的，从而就可以添加轴对称型全等三角形进行证明。由于图形中已经出现了对称轴CD，所以添加的方法是将三角形沿对称轴翻折，若考虑将△ACD沿CD翻折过去（如图5-20），则由∠BCD=∠ACD，可知CA必定落在CB上，所以具体的添加方法就是：在CB上截取CF=CA，再联结DF（如图5-20）。则由CF=CA，∠FCD=∠ACD和CD=CD，就可得△FCD≌△ACD，DF=DA。这样问题就转化成要证DE=DF，而这又是两条具有公共端点D的相等线段，它们可以组成一个等腰三角形，问题也就成为等腰三角形的判定问题，所以问题又应转化成证DE=DF的等价性质∠DEF=∠DFE。但我们已证∠DEF=80°，从而又应证∠DFE也等于80°，由于∠DFE是∠DFC的补角，而∠DFC=∠A=100°，所以分析可以完成。

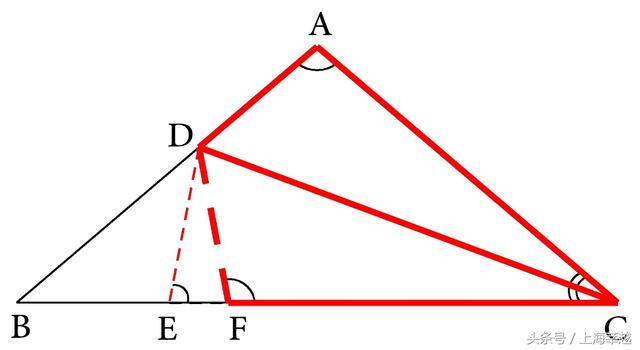
图5-20

本题在根据线段和差关系的定义来进行分析时，也可以考虑将CD和AD这两条线段接起来，也就是延长CD到E，使DE=DA（如图5-21），那么问题就成为要证CE=CB。但这是两条具有公共端点C的相等线段，它们可组成一个等腰三角形，于是联结BE（如图5-21），然后应证CE=CB的等价性质∠E=∠CBE。又因AB=AC，∠A=100°，所以∠ABC=∠ACB=40°，而CD是角平分线，所以∠BCD=20°那么问题也就是要证∠E=80°

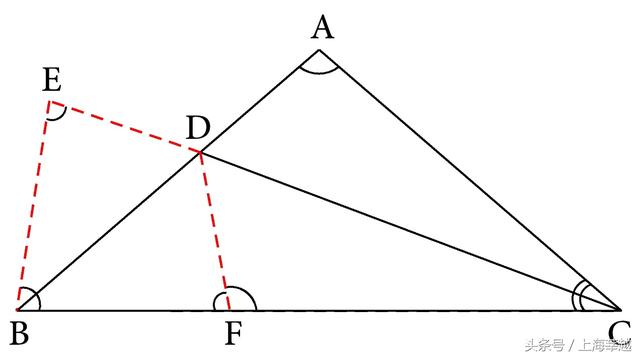
图5-21

由于∠BCD和∠ACD这两个相等的角是关于CD成轴对称的，所以可添加轴对称型全等三角形进行证明，于是在CB上截取CF=CA，并联结DF（如图5-21），即可得△ACD≌△FCD，DA=DF，∠DFC=∠A=100°，而B、F、C成一直线，所以∠BFD=80°，这样问题就是要证∠E=∠BFD，而这一性质也是等价于∠EBA=∠FBA=40°，所以△BDE和△BDF必定也是一对轴对称型全等三角形而在这两个三角形中，已经出现的条件是DE=DA=DF，DB=DB，所以还要证一个性质，由于上述已讨论的两组相等的角都是结论，不能用，所以只能证明第三个角，也就是这两条对应边的夹角相等，即要证∠BDE=∠BDF。由条件AB、CE相交于D，可得∠BDE=∠CDA。而在△ACD中，∠CDA=180°-100°-20°=60°，而∠CDF=∠CDA，所以∠BDF=180°-2×60°=60°，所以∠BDE=∠BDF可以证明，分析也就可以完成。