思考:如下图,观察山顶上的电视塔,站在斜坡上的什么位置,看到的电视塔最高?

数学家米勒简介:米勒(Johannes Miiller 1436——1476)德国数学家,对三角做出了巨大贡献。是欧洲最有影响的数学家之一。米勒发表的《三角全书》,是使得三角学在欧洲取得独立地位的第一部系统性著作。
米勒提出了一个有趣的问题:在地球表面什么部位,一根垂直的悬杆呈现最长?即在什么部位,视角最大?最大视角问题是数学史上100个著名的极值问题之一。
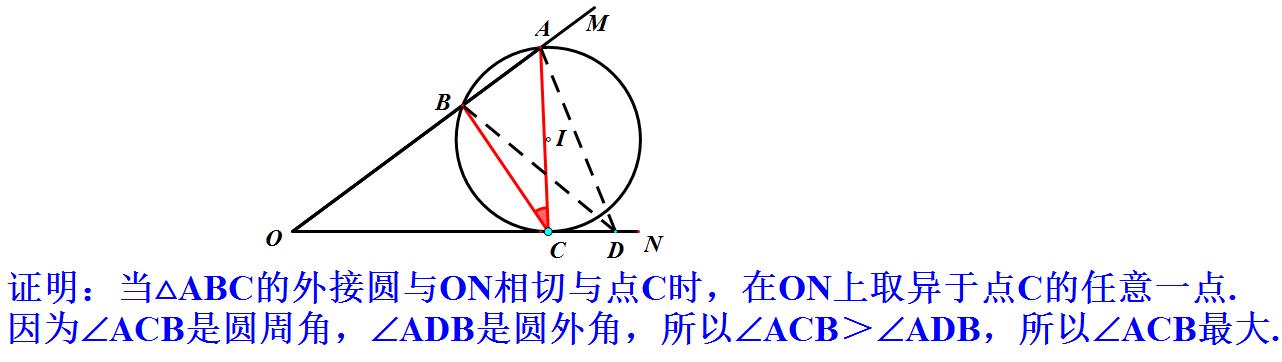
这一问题更一般的描述是:已知,点A、B是∠MON的ON边上的两个定点,C是OM边上的一个动点,当C在何处时,∠ACB最大?问题的答案是:当且仅当△ABC的外接圆与边OM相切于点C时,∠ACB最大。人们称这一命题为米勒定理!
一、米勒定理
1.探索:点C在运动的过程中,∠ACB的大小在不断发生变化。实验证明,当△ABC的外接圆与ON相切时,切点C使得∠ACB最大。
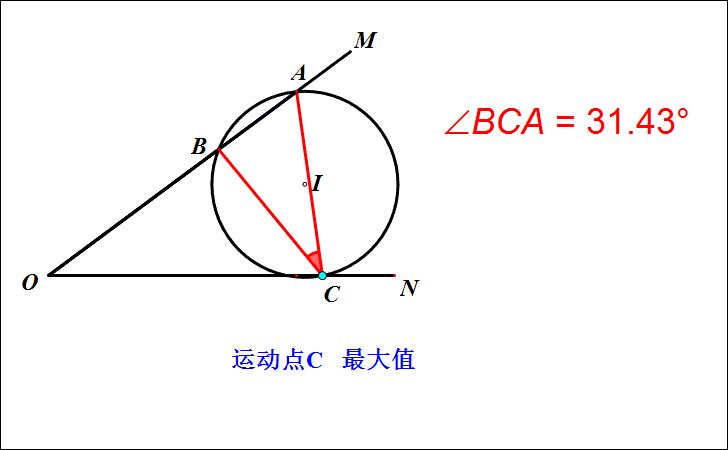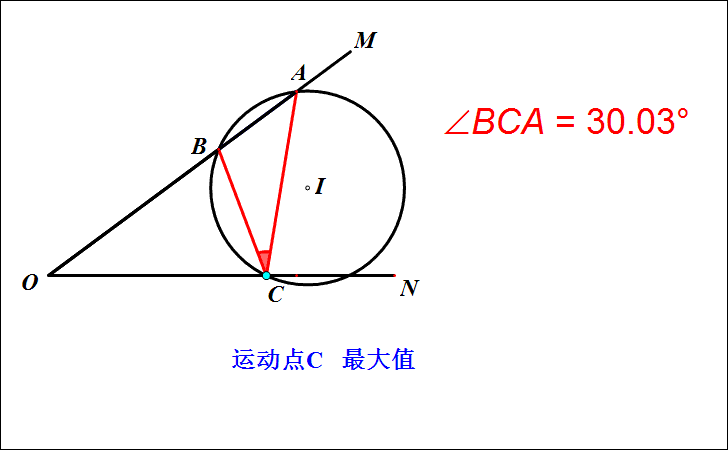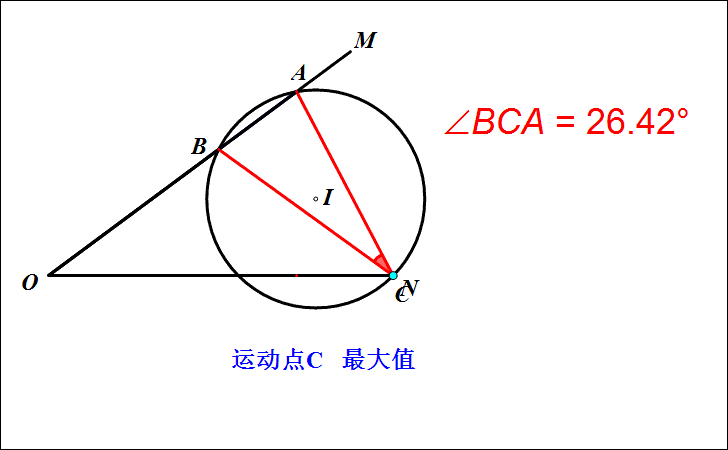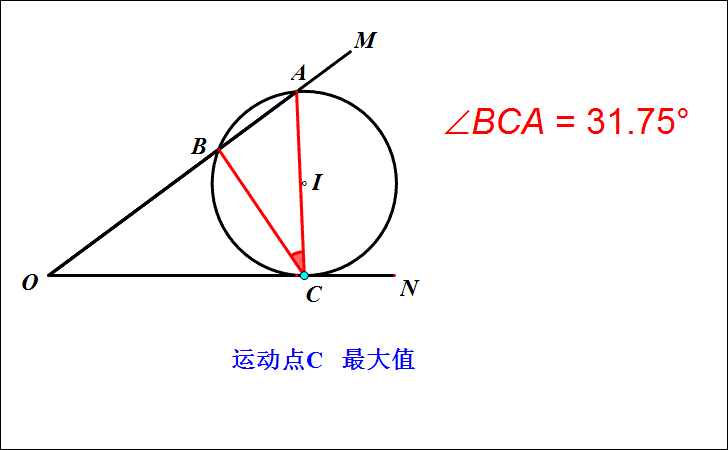
2.如何作出点C的位置?

3.定理的证明
二、应用练习

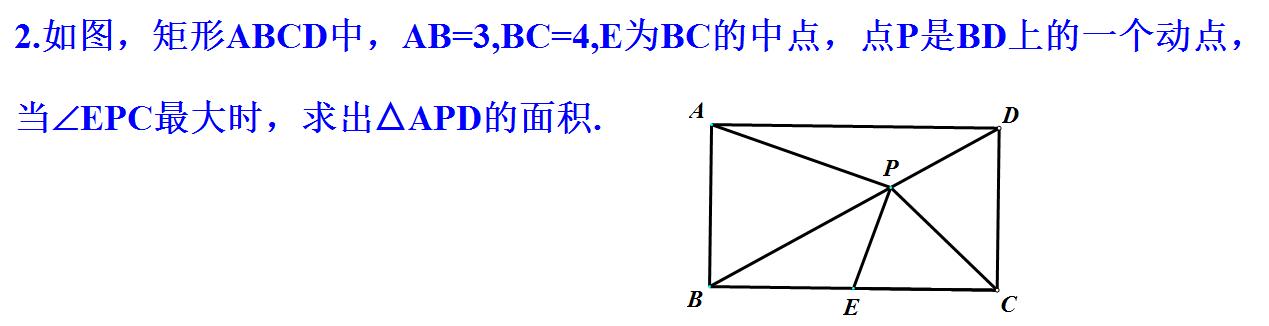
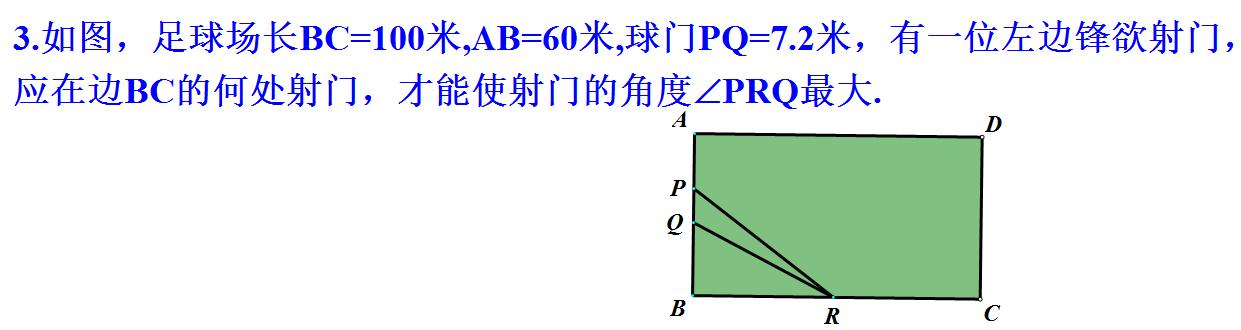

 加载中,请稍侯......
加载中,请稍侯......
精彩评论