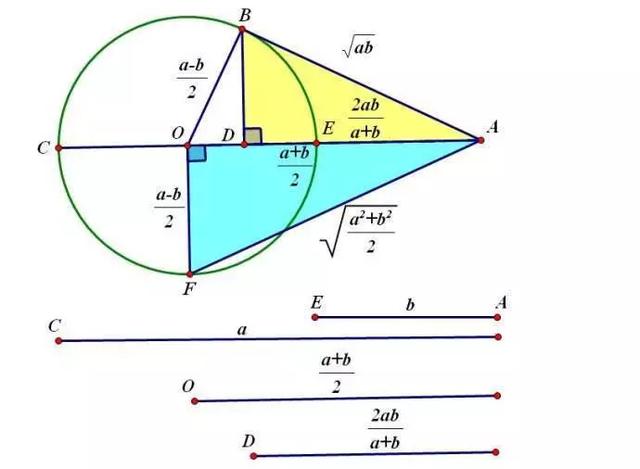
均值不等式历来是高考中的难点，本文将介绍一种可化为一次分式不等式的均值不等式的万能解法。该方法可覆盖高考中绝大多数的题型，且保证100%解出，但实际解题中，仍鼓励使用“技巧性”方法。

均值不等式解法中的常见错误

首先看一道例题：

若正数x,y满足x+2y=4xy，求x+y/2的最小值

以下是很多同学常见的错误解法：

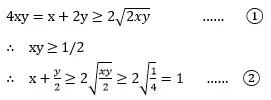
上述解法的错误在于将 x + 2y = 4xy 这个约束条件进行了放缩，所以结果并不符合约束条件的要求。

更明确的说：①式中等号成立的条件是x=2y，②式中等号成立的条件是x=y/2，所以按照约束条件的要求，x+y/2是无法取得上述最小值1的。

如何保留约束条件的完整信息是求解不等式问题的关键之一。

本例的技巧性解法如下：

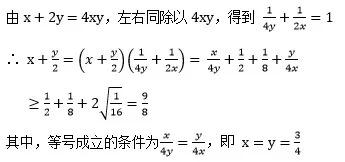
但技巧性解法千变万化，把握规律并不容易，一旦思路不畅，考场上可能浪费大量时间。

万能解法的思路

为了规避将约束条件放缩后导致的错误，所求式应尽量保留约束条件的一切信息，故可按照如下思路进行：

1.从约束条件推导任意未知数的表达式；

2.代入所求式，将所求式化为一次分式（此时也可通过导数求最值，但极不推荐。另，高次分式不等式不在本文讨论范畴）；

3.将分式凑成：常数+b/a+a/b 的形式；

4.利用均值不等式求得最值。

利用上述思路及方法考察例题：

首先，推导任意未知数表达式。如：可将x + 2y = 4xy 写成 x = 2y/(4y-1)。（此时保留了约束条件的一切信息）

代入所求式，化为一次分式，即：

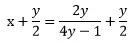
（此时可通过导数求最值，但不推荐，尽管此题利用导数求解也并不麻烦）

调整分式：

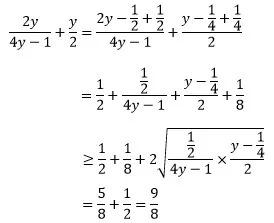
等号成立条件为：

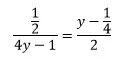
即：y=3/4。

万能解法一般代数形式

很多学生可能觉得，将分式凑成：常数+b/a+a/b的形式并不容易。当然这里需要一定的熟练度才能快速写出，但其本质是待定系数的思想，由此我们可以推导万能解法的一般代数形式。

对于形如：

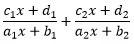
的一次分式，利用均值不等式求最小值的万能解法（其中分式中的分子和分母均为正数）。

如果要化成：常数+b/a+a/b 的形式，则需将c1x+d1化成m1(a1x+b1)+n1(a2x+b2)的形式，前半部分可以形成常数m1，后半部分可以利用均值不等式，与第二个分式的分母相消。故：

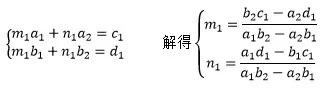
同理，将c2x+d2化成m2(a2x+b2)+n2(a1x+b1)，即：

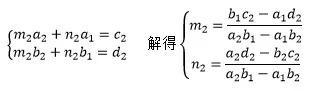
显然a1b2≠a2b1，否则这两个分式是可以合并同类项的。于是：

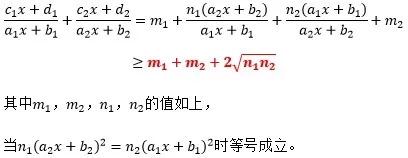
上述结论的代数形式复杂，仅供参考，万能解法的关键在于待定系数的思路及熟练拆分分子的方法。

应用实例

例：若正实数x,y满足2x+y+6=xy，则xy的最小值是多少？

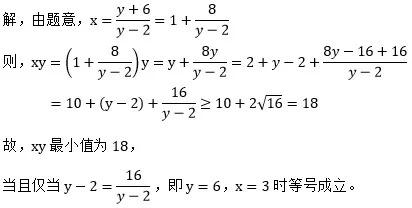
另，本题的其他主流解法为换元：令2x+y=p，xy=q，有能力的同学可以自行尝试。换元的关键同样在于如何保留约束条件的全部信息，换元之后只得到p+6=q是肯定不行的。

至于换元解不等式问题，另文再议。

提供几个习题，请尝试用万能解法求解：

1.已知x>0,y>0,x+2y+2xy=8,求x+2y的最小值（本题技巧性解法为换元，方法如上）

2.已知0<x<1 求5/(1-x)+3/x的最小值（本题技巧性解法为原式乘以（1-x+x））

3.若正数x,y满足x+3y=5xy,求3x+4y的最小值（本题技巧性解法为约束条件左右同除以xy，再乘到3x+4y中）

文|高见远，转载请注明出处。