与正方形有关的一类试题

【典型试题一】

【典型试题二】

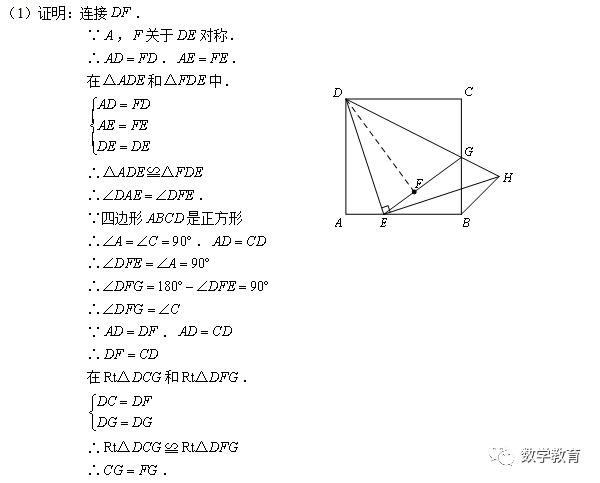
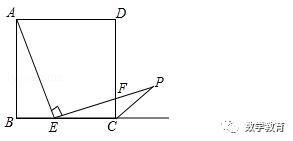
如图，在边长为3的正方形ABCD中，点E是BC边上的点，BE=1，∠AEP=90°，且EP交正方形外角的平分线CP于点P，交边CD于点F，

（1）FC/EF的值为；

（2）求证：AE=EP；

（3）在AB边上是否存在点M，使得四边形DMEP是平行四边形？若存在，请给予证明；若不存在，请说明理由．

【解析】（1）由正方形的性质可得：∠B=∠C=90°，由同角的余角相等，可证得：∠BAE=∠CEF，根据同角的正弦值相等即可解答；

（2）在BA边上截取BK=NE，连接KE，根据角角之间的关系得到∠AKE=∠ECP，由AB=CB，BK=BE，得AK=EC，结合∠KAE=∠CEP，证明△AKE≌△ECP，于是结论得出；

（3）作DM⊥AE于AB交于点M，连接ME、DP，易得出DM∥EP，由已知条件证明△ADM≌△BAE，进而证明MD=EP，四边形DMEP是平行四边形即可证出．

【典型例题三】

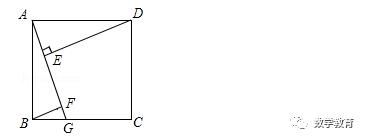
如图，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于E，BF∥DE，交AG于F．

（1）求证：AF﹣BF=EF；

（2）将△ABF绕点A逆时针旋转，使得AB与AD重合，记此时点F的对应点为点F′，若正方形边长为3，求点F′与旋转前的图中点E之间的距离．

【分析】（1）由四边形ABCD为正方形，可得出∠BAD为90°，AB=AD，进而得到∠BAG与∠EAD互余，又DE垂直于AG，得到∠EAD与∠ADE互余，根据同角的余角相等可得出∠ADE=∠BAF，利用AAS可得出三角形ABF与三角形ADE全等，利用全等三角的对应边相等可得出BF=AE，由AF﹣AE=EF，等量代换可得证。

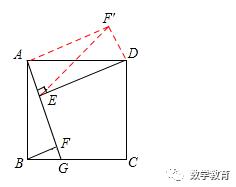
（2）将△ABF绕点A逆时针旋转，使得AB与AD重合，记此时点F的对应点为点F′，连接EF′，如图所示，由旋转的性质可得出∠FAF′为直角，AF=AF′，由（1）的全等可得出AF=DE，等量代换可得出DE=AF′=AF，再利用同旁内角互补两直线平行得到AF′与DE平行，根据一组对边平行且相等的四边形为平行四边形可得出AEDF′为平行四边形，再由一个角为直角的平行四边形为矩形可得出AEDF′为矩形，根据矩形的对角线相等可得出EF′=AD，由AD的长即可求出EF′的长。

解答：（1）证明：如图，∵正方形ABCD，∴AB=AD，∠BAD=∠BAG+∠EAD=90°。

∵DE⊥AG，∴∠AED=90°。∴∠EAD+∠ADE=90°。∴∠ADE=∠BAF。

又∵BF∥DE，∴∠AEB=∠AED=90°。在△AED和△BFA中，∵∠AEB=∠AED，∠ADE=∠BAF，AD = AB。

∴△AED≌△BDA（AAS）。∴BF=AE。

∵AF﹣AE=EF，∴AF﹣BF=EF。

（2）解：如图，

根据题意知：∠FAF′=90°，DE=AF′=AF，

∴∠F′AE=∠AED=90°，即∠F′AE+∠AED=180°。

∴AF′∥ED。∴四边形AEDF′为平行四边形。

又∵∠AED=90°，∴四边形AEDF′是矩形。

∴EF′=AD=3。

∴点F′与旋转前的图中点E之间的距离为3。