中考难点：动点轨迹与路径最值综合难题

对初中生来说，"轨迹"是一个比较抽象的问题，但在高中数学中的学习是非常有用的，也是非常重要的。在研究动点问题时，可以在运动中寻找不变的量，即不变的数量关系或位置关系。如果动点的轨迹是一条线段，那么其中不变的量便是该动点到某条直线的距离始终保持不变；如果动点的轨迹是一段圆弧，那么其中不变的量便是该动点到某个定点的距离始终保持不变．由于轨迹问题渗透着集合、运动和数形结合等重要思想，具有涉及面广，综合性强，技能要求高等特点，近年来，越来越多地出现在中考压轴题中.这类题型与通常给出图形的几何证明与计算题不同，需要经历一个"据性索图"的推理过程。因此，解决此类动点轨迹问题便可转化为寻找变量与不变的关系．

A、基本轨迹

符合一定条件的动点所形成的图形，或者说，符合一定条件的点的全体所组成的集合，叫做满足该条件的点的轨迹．六种常用的基本轨迹如下：

①到已知线段的两个端点距离相等的点的轨迹是这条线段的垂直平分线．

②到已知角的两边距离相等的点的轨迹是这个角的平分线．

③到已知直线的距离等于定长的点的轨迹是与这条直线平行，且与已知直线的距离等于定长的两条直线．

④到两条平行线距离相等的点的轨迹是和这两条平行线平行且到这两条平行线距离相等的一条直线．

⑤到定点的距离等于定长的点轨迹是与定点为圆心，定长为半径的圆．

⑥和已知线段的两个端点的连线的夹角等于已知角的点的轨迹是以已知线段为弦，所含圆周角等于已知角的两段弧(端点除外)．

B、常考类型

类型1、运动轨迹是线段

所谓单动点就是动点个数是一个，并且动点的轨迹是某条线段或者某条线段所在直线或射线，这类问题一般比较好处理，往往通过"垂线段最短"来处理，有时动点轨迹不容易确定，那么就需要同学们多观察，多与其他条件结合看，比如角平分线往往想到做垂直，但也可以利用角平分线的轴对称性来做对称变换，看到"中点"可以构造三角形的中位线或者想到"直角三角形斜边上的中线等于斜边的一般"，还可以构造八字形相似进行比例转换等。

1．（2019•温州一模）如图，△ABC是边长为6的等边三角形，点D在边AB上，AD＝2，点E是BC上一点，连结DE，将DE绕点D逆时针旋转60°得DF，连结CF，则CF的最小值为（ ）

A．2B．√3C．2√3-2D．6﹣3√3

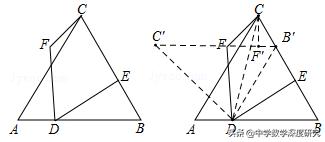
【分析】把△CDB绕点D逆时针旋转60°，得到△C′DB′，过点C作CF′⊥B′C′时，此时的CF′就是CF最小值的情况．因为等边△CBA底边AB上的高（点C到AB的距离）为3√3，根据CF′/3√3=CB′/CB=2/6，解得CF′值就是最小值．

【解答】把△CDB绕点D逆时针旋转60°，得到△C′DB′，

∵∠B＝∠BDB′＝60°，所以B′在BC上，BB′＝BD＝4．

∵∠C′B′D＝60°，∴∠CB′C′＝60°，∴B′C′∥AB．

过点C作CF′⊥B′C′时，此时的CF′就是CF最小值的情况．

∵等边△CBA底边AB上的高（点C到AB的距离）为3√3，

∴CF′/3√3=CB′/CB=2/6，，解得CF′＝√3．即CF最小值为√3．故选：B．

2．（2019•锡山区一模）如图，在平面直角坐标系中，已知A（4，6）、P(2，0)点C、B分别为x轴、y轴上的动点，构造△ABC，使∠BAC＝90°，若M为BC的中点，则PM的最小值为 _____

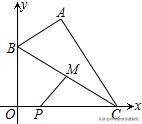
【解答】连接OM，AM，那么在点M的运动路线就是在线段AO的中垂线上，然后在利用点到直线的距离垂线段最短来处理。

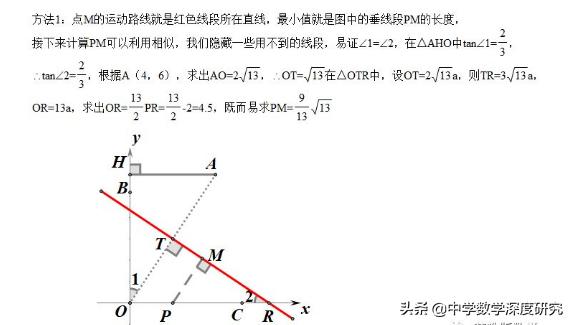
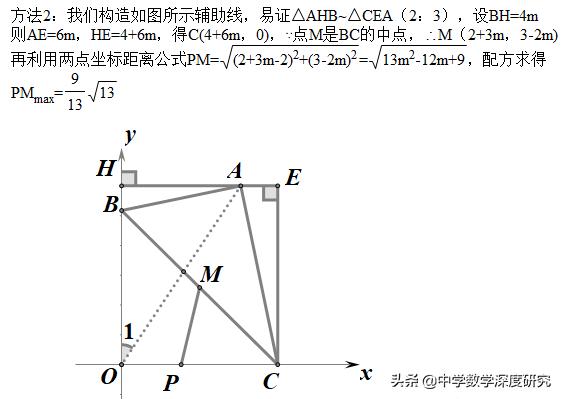
类型2、运动轨迹是圆弧

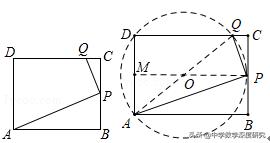
3．（2019•苍南县一模）如图，⊙O的半径为2，四边形ABCD为⊙O的内接矩形，AD＝6，M为DC中点，E为⊙O上的一个动点，连结DE，作DF⊥DE交射线EA于F，连结MF，则MF的最大值为（ ）

A．3√3+√69B．6+√51C．2√3+61√D．6√3

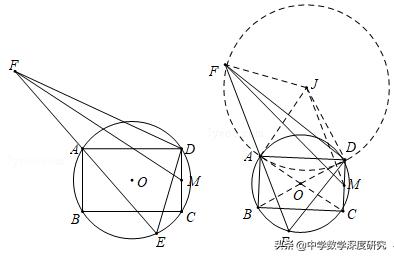
【分析】如图，连接AC交BD于点O，以AD为边向上作等边△ADJ，连接JF，JA，JD，JM．判断出点F的运动轨迹即可解决问题．

【解答】如图，连接AC交BD于点O，以AD为边向上作等边△ADJ，连接JF，JA，JD，JM．∵四边形ABCD是矩形，∴∠ADC＝90°，

∵AD﹣6，AC＝4，∴sin∠ACD＝AD/AC=6/2√3=√3，

∴∠ACD＝60°，∴∠FED＝∠ACD＝60°，

∵DF⊥DE，∴∠EDF＝90°，∴∠EFD＝30°，

∵△JAD是等边三角形，∴∠AJD＝60°，∴∠AFD＝1/2∠AJD，

∴点F的运动轨迹是以J为圆心JA为半径的圆，

∴当点F在MJ的延长线上时，FM的值最大，

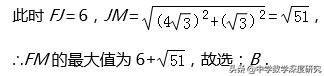
【点评】本题考查矩形的性质，等边三角形的性质和判定，点的运动轨迹等知识，解题的关键是正确寻找点F的运动轨迹，属于中考选择题中的压轴题．

4．（2019•江夏区模拟）如图，在直角坐标系中，等边△OAB的边OB在x轴的正半轴上，点A（3，m）（m＞0），点M，N分别从B、O出发，以相同的速度，沿BO，OA向O、A运动，连接AM、BN交于点E，点P是y轴上一点，则当EP最小时，点P的坐标是（ ）

A．（0，√3）B．（0，2√3）C．（0，3√3）D．（0，3√3、2）

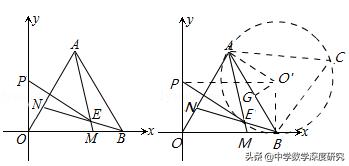
【分析】先判断出△OBN≌△MAB（SAS），即可判断出∠AEB＝120°，即可判断出点F是以O'为圆心的圆上的一段弧（劣弧AB），然后确定出圆心O'的位置及坐标，设出点M的坐标，即可确定当点P（0，2√3）时，EP的最小值是6﹣2√3．

【解答】如图，∵△OAB是等边三角形，

∴∠AOB＝∠ABM＝60°，OB＝AB，

∵点M、N分别从B、O以相同的速度向O、A运动，

∴BM＝ON，在△OBN和△MAB中，ON=BM, ∠BON＝∠ABM＝60°，OB=AB,

∴△OBN≌△MAB（SAS），∴∠OBN＝∠BAM，

∴∠ABN+∠BAM＝∠ABN+∠OBN＝∠ABO＝60°

∴∠AEB＝180°﹣（∠ABN+∠BAM）＝120°，

∴点E是经过点A，B，E的圆上的点，记圆心为O'，在⊙O'上取一点C，使点C和点E在弦AB的两侧，连接AC，BC，∴∠ACB＝180°﹣∠AEB＝60°，

连接O'A，O'B，∴∠AO'B＝2∠ACB＝120°，

∵O'A＝O'B，∴∠ABO'＝∠BAO'，

∴∠ABO'＝1/2（180°﹣∠AO'B）＝1/2（180°﹣120°）＝30°，

∵∠ABO＝60°，∴∠OBO'＝90°，

∵△AOB是等边三角形，A（3，m），∴AB＝OB＝2×3，m＝3√3，

过点O'作O'G⊥AB，∴BG＝1/2AB＝3，

在Rt△BO'G中，∠ABO'＝30°，BG＝3，

【点评】此题是圆的综合题，主要考查了等边三角形的性质，全等三角形的性质和判定，勾股定理等知识点；找出点E的运动轨迹是解本题的关键也是难点．解此类题目的方法是判断出动点的轨迹所在的圆的圆心和确定出半径．

C、牛刀小试

1．（2018秋•梁子湖区期末）如图，△ABC和△ADE都是等腰直角三角形，且∠BAC＝∠DAE＝90°，BC＝4，O为AC中点．若点D在直线BC上运动，连接OE，则在点D运动过程中，线段OE的最小值为（ ）

A．0.5 B．1 C．1.5 D．2

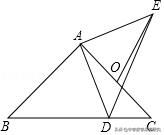
【解析】取AB的中点Q，连接DQ，先证得△AQD≌△AOE，得出QD＝OE，根据点到直线的距离可知当QD⊥BC时，QD最小，然后根据等腰直角三角形的性质求得QD⊥BC时的QD的值，即可求得线段OE的最小值为1故选：B．

2．（2019•惠山区一模）如图，正方形ABCD中，AB＝2√5，O是BC边的中点，点E是正方形内一动点，OE＝2，连接DE，将线段DE绕点D逆时针旋转90°得DF，连接AE，CF．则线段OF长的最小值（ ）

A．2√5 B．√5+2 C．2√10﹣2 D．5√2-2

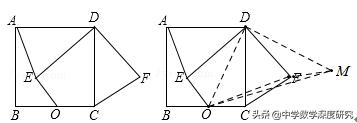
【解析】连接DO，将线段DO绕点D逆时针旋转90°得DM，连接OF，FM，OM，证明△EDO≌△FDM，可得FM＝OE＝2，由条件可得OM＝5√2，根据OF+MF≥OM，即可得出OF≥5√2 -2．故选：D．

3．（2019•东台市模拟）如图，Rt△ABC中，∠ACB＝90°，AC＝BC＝4，D为线段AC上一动点，连接BD，过点C作CH⊥BD于H，连接AH，则AH的最小值为______ ．

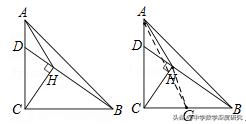
【解析】取BC中点G，连接HG，AG，由直角三角形的性质可得HG＝CG＝BG＝1/2BC＝2，由勾股定理可求AG＝2√5，由三角形的三边关系可得AH≥AG﹣HG，当点H在线段AG上时，可求AH最小值为2√5﹣2．

4．（2019春•海淀区校级月考）在平面直角坐标系xOy中，点A（1，1），C（﹣1，﹣1）．⊙A，⊙C的半径均为1，平行四边形MONP的顶点M，N分别在⊙A，⊙C上，则线段OP长度的最大值为 ______．

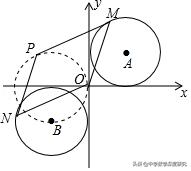
【解析】如图，∵四边形MONP是平行四边形，点M在⊙A上运动，

∴点P的运动轨迹也是圆，圆的半径与⊙A的半径相等，直径为2，

∴当OP为直径时，OP的值最大，最大值为2．故答案为2．

5．（2019•碑林区校级一模）如图，正方形ABCD的边长为2√3，点E为正方形外一个动点，∠AED＝45°，P为AB中点，线段PE的最大值是 ______．

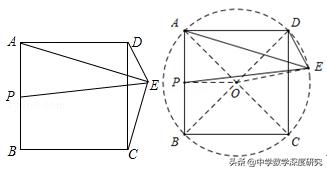
【解析】连接AC，BD交于点O，连接PO，EO，根据A，C，E，D四点共圆，可得OE＝OD＝1/2BD＝√6，再根据PE≤OP+OE＝√6+√3，可得当点O在线段PE上时，PE＝OP+OE＝√6+√3，则线段PE的最大值为√6+√3．

6．（2019•武汉模拟）如图，在矩形ABCD中，AB=5/2，点P是BC边上的一动点（不与B，C重合），PQ⊥AP交边CD于点Q，若CQ的最大值为2/5，则AD的长为_______ ．

【解析】连接AQ，则点A，D，Q，P在以AQ为直径的⊙O上，

∵点P是BC上一动点，∴当⊙O与BC相切于点P时，CQ最大，

连接PO并延长AD交于点M，则OM⊥AD，

∵CQ=2/5，∴OM=1/2DQ=21/20，OP=OA=MP-OM=29/20，

在Rt△AOM中，由勾股定理可求得AM=1，∴AD＝2AM＝2．

D.方法总结

对于初中数学中动点轨迹的问题，一般有两种情况：线段或圆弧。在研究动点问题时，可以在运动中寻找不变的量，即不变的数量关系或位置关系：如果动点的轨迹是一条线段，那么其中不变的量便是该动点到某条直线的距离始终保持不变；如果动点的轨迹是一段圆弧，那么其中不变的量便是该动点到某个定点的距离始终保持不变。因此，解决此类动点轨迹问题便可转化为寻找定直线或定点。

由此可归纳为轨迹问题三部曲：猜测轨迹形状——证明轨迹形状——代入图形应用其中第二步很重要，初中证明轨迹有两种证明方法：几何法和解析法。所谓几何法就是通过纯几何证明，抓紧不变量，得出轨迹形状，一般是圆或直线（线段）。进一步简化，就是在研究轨迹问题时，需要找到三个静止的点，合情推理出轨迹形状，然后进行逻辑推理证明角的度数，从而计算出轨迹长度。