中考：线段差的最大值问题探究

求形如|PA-PB|的最大值问题

模型特点：图形中一般出现三个点，多为“两定一动型”，要求“两条线段差的最大值”.

解决方法：化曲为直，利用对称或延长，使几个线段或对应点成一直线。

若点A和B是定点，点P为直线l上一动点，分以下两种情况探究

【情况一】

点A和点B在直线l同侧，连接AB并延长交直线l于点P，此时|PA-PB|有最大值.

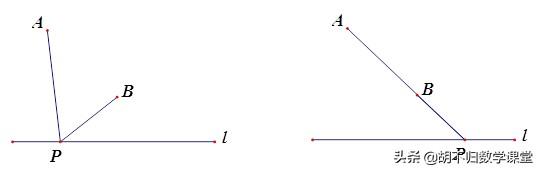
【情况二】

点A和B在直线l异侧，作点B关于直线l的对称点B’， 连接AB’并延长交直线l于点P，此时|PA-PB|有最大值.

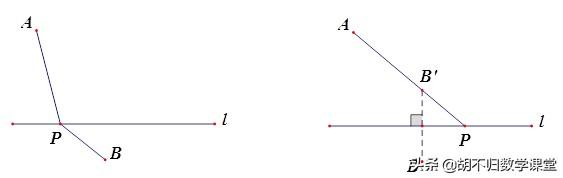
【典例】

1、已知，如图点A(1,1),B(2,-3),点P为轴上一点，当|PA-PB|最大时，点P的坐标为________

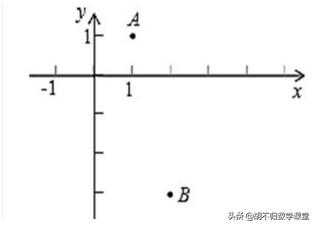
解析：“将军饮马问题”，选择压轴题。如下图，依“两边之差小于第三边”可知：|PA-PB|<AB，当P、A、B在同一直线上时，|PA-PB|=|PA`-PB|=A`B,有最大值。∴作点B关于x轴的对称点B`，连接B`A并延长交x轴于点P，∵A`(1,-1),B(2,-3)，∴直线A`B的解析式为：y=-2x+1，当y=0时x=0.5,∴P(0.5,0).

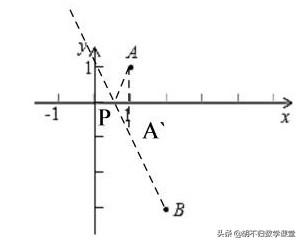
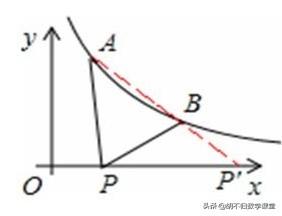
2、如图，已知A(0.5,y1)，B(2,y2)为反比例函数y=1/x的图像上的两点，动点P(x,0)在x轴的正半轴上运动，当|PA-PB|最大时，点P的坐标是_________

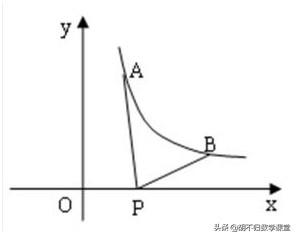
解析： A（0.5，2），B（2，0.5）。∵在△ABP中，由三角形的三边关系定理得：|AP－BP|＜AB，如下图，延长AB交x轴于P′，当P在P′点时，PA－PB=AB，即此时线段AP与线段BP之差达到最大。设直线AB的解析式是y=kx+b，把A、B的坐标代入得：直线AB的解析式是y=-x+2.5,∴P(2.5,0).

3、已知如图，直线y=-0.75x+6与x、y轴的交点分别为A、B，将∠OBA对折，使点O的对称点H落在直线AB上，折痕交x轴于点C.

（1）直接写出点C的坐标，并求过A、B、C三点的抛物线的解析式；

（2）设抛物线的对称轴与直线BC的交点为T，Q为线段BT上一点，直接写出|QA-QO|的取值范围。

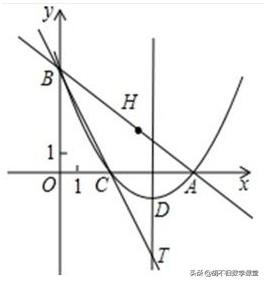
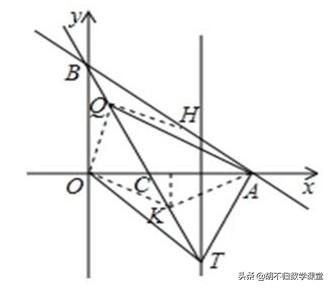
解析：（1）点C的坐标为（3，0）,∵点A、B的坐标分别为A（8，0），B（0，6）,∴可设过A、B、C三点的抛物线的解析式为y=a（x-3）（x-8），将x=0，y=6代入抛物线的解析式，得a=1/4. ∴过A、B、C三点的抛物线的解析式为y=1/4x*2-11/4x+6.

（2）|QA-QO|的取值范围是0≤|QA-QO|≤4.

当Q在OA的垂直平分线上与直线BC的交点时，（如点K处），此时OK=AK，则|QA-QO|=0.

当Q在AH的延长线与直线BC交点时，此时|QA-QO|最大.

直线AH的解析式为：y=-0.75x+6，直线BC的解析式为：y=-2x+6, 联立可得：交点为（0，6）, ∴OQ=6，AQ=10, ∴|QA-QO|=4, ∴|QA-QO|的取值范围是：0≤|QA-QO|≤4.

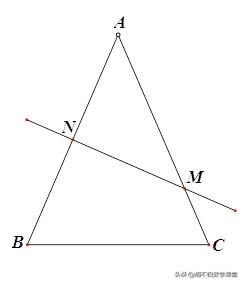
【练习】如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交AC于点M.

（1）若∠B=65º，则∠NMA=_______º；

（2）探究∠B与∠NMA的关系，并说明理由；

（3）连接MB，若AB=8cm，△MBC的周长是14cm，在直线MN上是否存在点P，使PB-CP的值最大？若存在，画出点P的位置，并求出最大值；若不存在，说明理由.