掌握好这5点，一次函数从此无难题

1.函数自变量的取值范围

自变量的取值范围必须使含有自变量的表达式都有意义．

①当表达式的分母不含有自变量时，自变量取全体实数．例如y=2x+13中的x．

②当表达式的分母中含有自变量时，自变量取值要使分母不为零．例如y=x+2x﹣1．

③当函数的表达式是偶次根式时，自变量的取值范围必须使被开方数不小于零．

④对于实际问题中的函数关系式，自变量的取值除必须使表达式有意义外，还要保证实际问题有意义．

2.一次函数的应用

1、分段函数问题

分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符合实际．

2、函数的多变量问题

解决含有多变量问题时，可以分析这些变量的关系，选取其中一个变量作为自变量，然后根据问题的条件寻求可以反映实际问题的函数．

3、概括整合

（1）简单的一次函数问题：①建立函数模型的方法；②分段函数思想的应用．

（2）理清题意是采用分段函数解决问题的关键．

3.待定系数法求一次函数解析式

待定系数法求一次函数解析式一般步骤是：

（1）先设出函数的一般形式，如求一次函数的解析式时，先设y=kx+b；

（2）将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；

（3）解方程或方程组，求出待定系数的值，进而写出函数解析式．

注意：求正比例函数，只要一对x，y的值就可以，因为它只有一个待定系数；而求一次函数y=kx+b，则需要两组x，y的值．

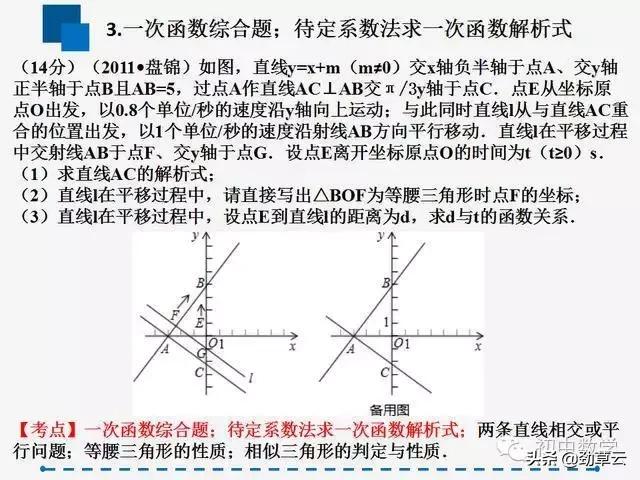
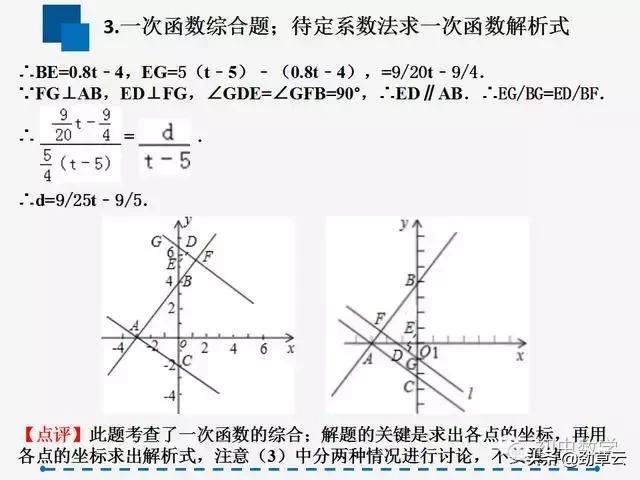
3.一次函数综合题

（1）一次函数与几何图形的面积问题

首先要根据题意画出草图，结合图形分析其中的几何图形，再求出面积．

（2）一次函数的优化问题

通常一次函数的最值问题首先由不等式找到x的取值范围，进而利用一次函数的增减性在前面范围内的前提下求出最值．

（3）用函数图象解决实际问题

从已知函数图象中获取信息，求出函数值、函数表达式，并解答相应的问题

4.一次函数与一元一次不等式

（1）一次函数与一元一次不等式的关系

从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；

从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．

（2）用画函数图象的方法解不等式kx+b＞0（或＜0）

对应一次函数y=kx+b，它与x轴交点为（﹣b/k，0）．

当k＞0时，不等式kx+b＞0的解为：x＞﹣bk，不等式kx+b＜0的解为：x＜﹣bk；

当k＜0，不等式kx+b＞0的解为：x＜﹣bk，不等式kx+b＜0的解为：x＞﹣bk．

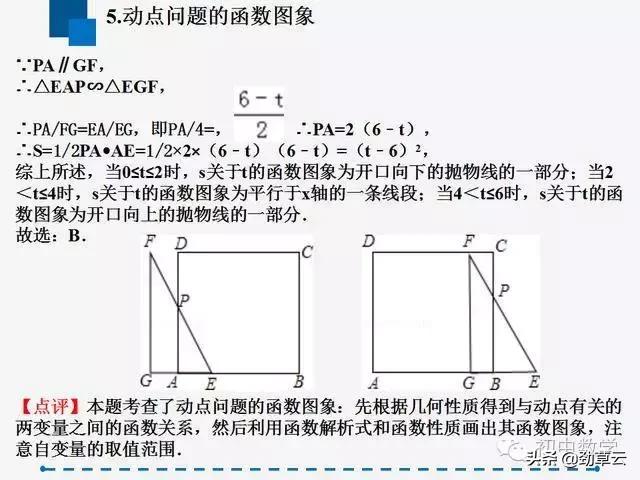
5.动点问题的函数图象

函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．

用图象解决问题时，要理清图象的含义即会识图．