直线与抛物线唯一公共点的深入理解

2019年武汉市中考数学压轴题，同样也考察了直线与抛物线有唯一公共点的情形，但本题特殊之处在于，不需要和以往类型的题目那样，通过联立方程，求根的判别式，逆推法同样可行。对于函数综合中的几何部分，融合得较好。最后一问看上去毫无头绪，实际上，只要对直线与抛物线有唯一公共点有深入理解，几乎可以秒答。

题目

已知抛物线C1:y=(x-1)²-4和C2:y=x²

(1)如何将抛物线C1平移得到抛物线C2？

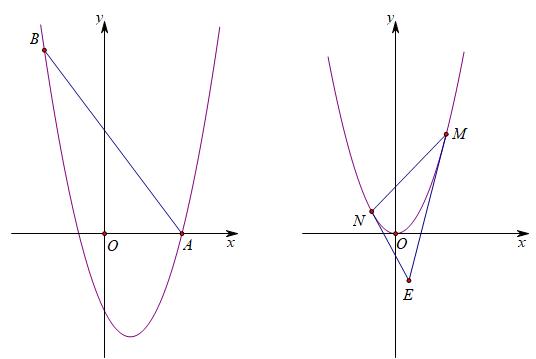
(2)如图1，抛物线C1与x轴正半轴交于点A，直线y=-4/3x+b经过点A，交抛物线C1于另一点B。请你在线段AB上取点P，过点P作直线PQ∥y轴交抛物线C1于点Q，连接AQ

①若AP=AQ，求点P的横坐标；

②若PA=PQ，直接写出点P的横坐标；

(3)如图2，△MNE的顶点M，N在抛物线C2上，点M在点N右边，两条直线ME、NE与抛物线C2均有唯一公共点，ME、NE均与y轴不平行。若△MNE的面积为2，设M、N两点的横坐标分别为m、n，求m与n的数量关系。

解析：

(1)送分题，比较两抛物线的顶点坐标，由(1,-4)到(0,0)，向左1个单位，向上4个单位；

(2)先按要求作出线段AB上的点P，它在不同位置，对应本小题的①和②，当然，前期准备工作必不可少，我们先求直线解析式，由抛物线C1与x轴交点，求出点A(3,0)，再将点A(3,0)代入y=-4/3x+b，求出b=4，于是y=-4/3x+4：

①AP=AQ，显然△APQ为等腰三角形，如下图：

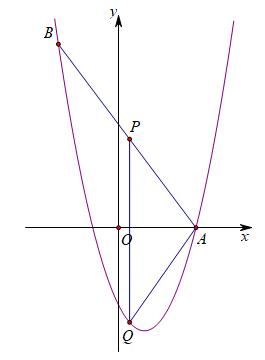
于是点P和点Q纵坐标互为相反数，抓住这一数量关系，我们列方程特别简单。设P(p，-4/3p+4)，Q(p，(p-1)²-4)，于是得到-4/3p+4+(p-1)²-4=0，整理得3p²-10p+3=0，解得p=1/3；

②PA=PQ，显然△APQ仍然是等腰三角形，不过腰为PA和PQ，如下图：

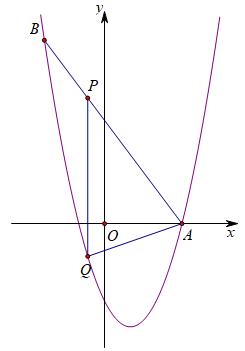
我们依然可设P(p,-4/3p+4)，Q(p,(p-1)²-4)，于是PQ=-4/3p+4-(p-1)²-4，在求AP的长时，其实可以利用三角函数，直线斜率为-4/3，因此tan∠PAO=4/3，于是得到AP=5/4(-4/3p+4)=-5/3p+5，可列方程-4/3p+4-(p-1)²-4=-5/3p+5整理得3t²-7t-6=0，解得p=-2/3；

(3)先研究直线与抛物线有唯一公共点时，我们通常做的事，就是联立方程，而这个方程(一般是一元二次方程)有两个相等的实数根，我们的切入点就选在这里。

点M的横坐标m一定是这个方程的根，且就是那两个相等的实数根，而联立方程的化简后最终结果一定是(x-m)²=0，将它展开，并“还原”成联立方程的初始状态，得x²=2mx-m²，左边是抛物线的含自变量部分，右边一定是直线的自变量部分，所以可以得到直线EM为y=2mx-m²，同理直线EN为y=2nx-n²，点E是它们的交点，联立方程得2mx-m²=2nx-n²，整理得x=(m+n)/2，于是得到点E((m+n)/2,mn)，至此E、M、N坐标全部都用含m、n的代数式表示出来，我们开始表示△EMN的面积，如下图：

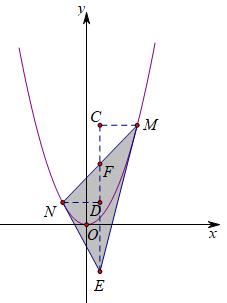
从刚才的推导过程中，我们其实可以发现，点E的横坐标恰为M、N横坐标和的一半，因此过点E作EF∥y轴，它与MN的交点F一定是中点，即F((m+n)/2,(m²+n²)/2)，而CM+DN=m-n，所以△EMN的面积可表示为1/2EF(m-n)，把EF=(m²+n²)/2-mn代入，整理后得m-n=2.

解题反思：

作为二次函数压轴题，起手很容易，考察了坐标系内的平移，过渡部分很平稳，选择了等腰三角形的存在性，并且还不需要进行分类讨论，甚至第二个P点坐标可以直接写出来。而本题精华自然是最后一问，我在第一眼看到它之后，下意识便开始用字母表示M点坐标，设E点坐标，然而1分钟后便醒悟了，这样的计算量是否太大？然后在思考唯一公共点时，想到了判别式，想到了唯一交点，想到了两个相等的实数根，最后便有了上述解法，而在△EMN的面积处理时，并没有采用补成梯形的方法，而是直接用EF分割成两个三角形，割补法，通常能割就能补。

想通了这一层之后，再回顾这道题，瞬间感觉很简单，这种简单的基础，是对唯一公共点的深入理解，以及对斜率、三角函数的熟练运用，函数综合题，谁能高效使用这些知识，便是胜者。