聚焦勾股定理中的数学思想

一、方程思想

所谓方程思想，就是通过观察，分析，判断，从已知量和未知量之间的位置关系或数量关系入手，找出等量关系，运用数学符号语言将相等关系转化为方程，再通过解方程把问题解决.

例1 如图，将矩形纸片ABCD的一边AD向下折叠，点D落在边BC上的F处，已知AB=8,AD=10.求CE得长。

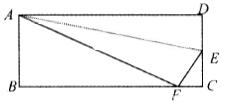
点评 通过勾股定理来建立方程是数学中常用的思想方法，设未知数把未知的量与已知的量集中到一个直角三角形中，再通过勾股定理建立方程，然后再解方程求出CE的长.

二、数形结合思想

所谓数形结合思想:就是将抽象的数学语言与直观的图形结合起来，使抽象思维和形象思维结合起来，通过“以形助数”，和“以数辅形”，使复杂问题简单化，抽象问题具体化.

例2 如图:正方形网格中，每个小正方形的边长为1，则网格上的△ABC中，边长是无理数的边数有( )条

A.0 B. 1 C.2 D. 3

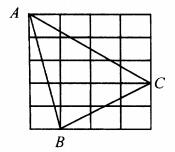
点评 勾股定理由已知的“直角三角形”得出“a²+b²=c²”的结论，这是由“形”的条件而得出“数”的结果，蕴含着从形到数的转化.

三、分类讨论思想

所谓分类讨论思想，就是将问题划分为若干个既不重复也不遗漏的小问题，再一一加以解决的方法.当问题的条件不具体时，通过分类讨论可以确定准确的答案.

例3 在△ABC中，AB=15,AC=13，边BC上的高AD=12.求△ABC的面积.

点评 本题△ABC的形状不确定，可以通过分类讨论来解决问题.

四、转化思想

所谓转化思想，就是将要解决的问题转化为另一个较为容易解决的问题或已经解决的问题，具体的做法是将未知的“转化”为“已知”，将“陌生”的转化为“熟悉”，将“复杂”的转化为“简单”.

例4 如图:要在直线L上修一水利站，分别向张庄A和李庄B送水，已知张庄A到河边L的距离AC= 2km，李庄B到河边L的距离BD=7km,CD=12km.如果铺设水管的工程费用为每千米1500元，求铺设水管的最小费用.

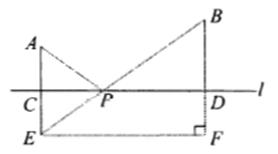
点评 遇到实际问题或非直角三角形时，通常把实际问题或非直角三角形转化为直角三角形，然后利用勾股定理来解决问题.