题中无圆 心中有圆

初中数学中有些问题看似与圆无关，而用题设条件又不好入手时，可挖掘题中条件，构造辅助圆，往往能“柳暗花明”，笔者总结了当条件中出现以下三种情况时，可考虑构造辅助圆，帮助我们有效地解题．

一、条件中有一锐角为45°时，可考虑构造辅助圆

例1 如图1，在△ABC中，AD⊥BC于点D，∠BAC＝45°，BD＝3，CD＝2．求△ABC的面积．

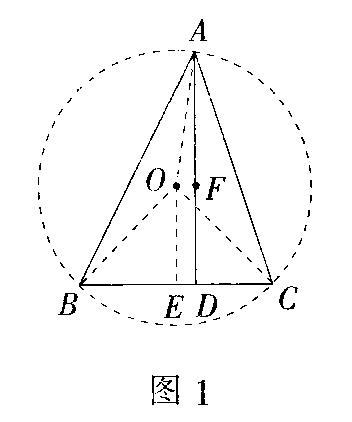
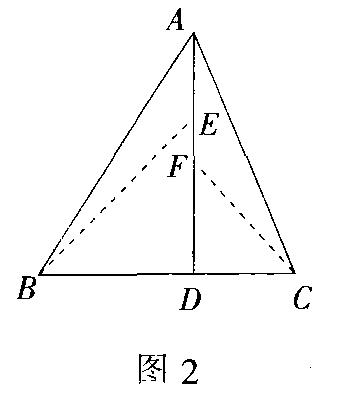
分析 本题主要求出△ABC的高AD即可获解，而利用“∠BAC＝45°’这个条件是关键，不妨构造辅助圆．让∠BAC变为圆周角，那么圆心角∠BOC为90°，这时△BOC为等腰直角三角形了，再利用圆的有关知识就可求出高AD了．

解 如图1，作△ABC的外接圆O．过点O作OE⊥BC，于点E，由∠BAC＝45°知∠BOC为90°，则△OBE、△OBC均为等腰直角三角形，且OE＝EC＝BE＝2.5，则ED＝CE－CD＝0.5，过点O作OF⊥AD于点F，连OA，则四边形OEDF为矩形，于是OF＝DE＝0.5，DF＝OE＝2.5．在Rt△AOF中，由勾股定理AF＝3.5，所以AD＝AF＋FD＝6，即S△ARC＝½×5×6＝15．

二、条件中有共顶点的两边或三边相等时，可考虑构造辅助圆

例2 在四边形ABCD中，∠BAD＝100°，∠BCD＝130°，AB＝AD＝2，求AC．

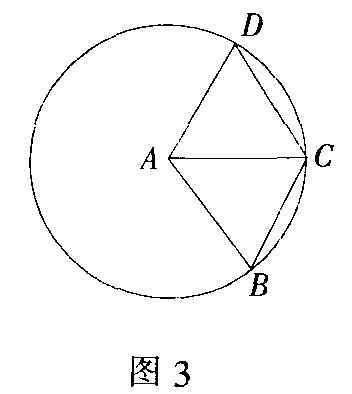
解 如图3，以点A为圆心，AB为半径作⊙A．则点D在圆上，由∠BAD＝100°知弧BMD的度数为260°，正好为∠BCD度数的2倍，故点C在⊙A上，所以AC＝2．

例3 在四边形ABCD中，AB∥CD，AD＝DC＝DB＝2，BC＝√7．求对角线AC的长．

分析 由“AD＝DC＝DB＝2”可知A、B、C在半径为2的⊙D上．利用圆的性质可找到AC与CD、BC的关系

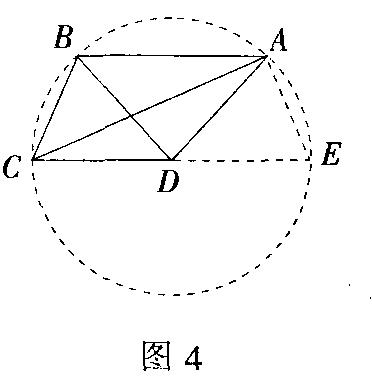
解 如图4，延长CD交半径为2的⊙D于点E，连AE，显然点A、B、C在⊙上，因AB∥CD，则

弧BC＝弧AE,从而BC＝AE＝√7．在△ACE中，∠BOC＝90°，CE＝4，AE＝√7，故AC＝3．

三、条件中有一角是另一角的2倍时，可考虑构造辅助圆

例4 （2001年全国初中数学竞赛）如图5，在△ABP中，PA＝PB，∠APB＝2∠ACB，AC与PB交PB于点D，且PB＝4，PD＝3，则AD·DC等于( )

(A)6 (B)7 (C)12 (D)16

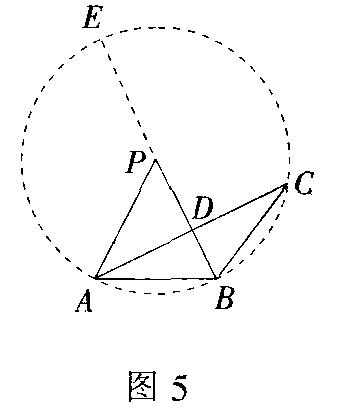
分析 构造以点P为圆心，PA为半径的⊙P．由“∠APB＝2∠ACB”可知点C在⊙O上．利用圆的有关性质可求出AD·DC的值．

解 如图5，延长BP交OP于点E，由相交弦定理，得AD·DC＝DE·DB

＝(PE＋PD)·(PB－PD)＝(4＋3)(4－3)＝7．

故选 B．