一,二次函数y=a(x+h)²+k的图像和性质
1.二次函数y=a(x+h)²+k的图像是一条抛物线,它的顶点是(-h,k) 对称轴是x=-h
当a>0时,图像开口向上,有最低点,即顶点是(-h,k) 当x=-h时,y有最小值为k;在对称轴的左侧,y随x的增大而减小,在对称轴的右侧,y随x的增大而增大。
当a<0时,图像开口向下,有最高点,即顶点是(-h,k) 当x=-h时,y有最大值为k;在对称轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小。
2.抛物线y=a(x+h)²+k与y=ax²的关系
抛物线y=a(x+h)²+k可由抛物线y=ax²平移得到,它们的形状相同,位置不同。
把y=ax²的图像先沿着x轴向左(或向右)平移|h|个单位后,得到y=a(x±h)²的图像;再沿着y轴向上(或向下)平移|k|个单位,得到y=a(x±h)²+k的图像。
例如y=3(x-2)²+1的图像是由抛物线y=3x²向右平移2个单位,再向上平移1个单位得到的。
注意:y=ax²上、下平移后得到y=ax²±k的规律是“上加下减”
y=ax²左、右平移后得到y=a(x±h)²的规律是“左加右减”
3.由于从y=a(x+h)²+k(a≠0)中,可直接看出抛物线的顶点坐标,所以把y=a(x+h)²+k(a≠0)叫做二次函数 的顶点式;把y=ax²+bx+c(a≠0)叫做二次函数的一般式。
注意:顶点决定抛物线的位置,几个不同的二次函数,如果二次项系数a相同,那么抛物线开口方向,开口大小完全相同,只是顶点不同。
例如:y=3x²与y=3x²+1、y=3x²+2x等只是顶点位置不同。
抛物线的移动主要看顶点的移动,如:y=3x²与y=(x+1)²+3的位置关系,先求出顶点,y=3x²的顶点坐标是(0,0),y=(x+1)²+3的顶点坐标是(-1,3),平移时与上、下、左、右的先后顺序无关。
二,二次函数的一般式y=ax²+bx+c与二次函数的顶点式y=a(x+h)²+k的相互转化
1.顶点式y=a(x+h)²+k转化一般式y=ax²+bx+c
例如:y=(x-1)²+2 (顶点式)
=x²-2x+1+2
=x²-2x+3 (一般式)
解题技巧:将顶点式中的括号打开,再进行合并同类项。
2.一般式y=ax²+bx+c转化顶点式y=a(x+h)²+k
y=ax²+bx+c
=a[x²+(b/a)x+(c/a)]
=a[x²+2(b/2a)x+(b/2a)²-(b/2a)²+(c/a)]
=a[x+(b/2a)]²+(4ac-b²)/4a
令h=b/2a,k=(4ac-b²)/4a,则y=a(x+h)²+k
因此,抛物线y=ax²+bx+c的对称轴是x=-b/2a ,顶点坐标[-b/2a,(4ac-b²)/4a]
解题技巧:利用配方法在一般式加上一次项系数一半的平方,再减去一次项系数一半的平方,这样一加一减,与原来式子恒等。
三,求抛物线的顶点和对称轴的方法
1.公式法:y=ax²+bx+c
= a[x+(b/2a)]²+(4ac-b²)/4a
顶点坐标[-b/2a,(4ac-b²)/4a] 对称轴是x=-b/2a
2 .配方法:将抛物线的关系式化为 y=a(x+h)²+k ,得到顶点为(-h,k),对称轴是直线x=-h
四,二次函数y=ax²+bx+c图像的画法
1.描点法:把二次函数y=ax²+bx+c化为 y=a(x+h)²+k的形式;确定抛物线的开口方向、对称轴、顶点坐标;在对称轴两侧,以顶点为中心,左右对称描点画图。
注意:若抛物线与x轴有交点,最好选取交点描点,特别是在画抛物线草图时,应注意以下各项:
开口方向、顶点、对称轴、与x轴的交点、与y轴的交点。
2.平移法:利用配方法把二次函数y=ax²+bx+c化为 y=a(x+h)²+k的形式,确定其顶点(-h,k);画出y=ax²的图像;将抛物线y=ax²的图像平移,使其顶点平移到(-h,k)。
注意:平移图像的基本要点:上加下减、左加由减。
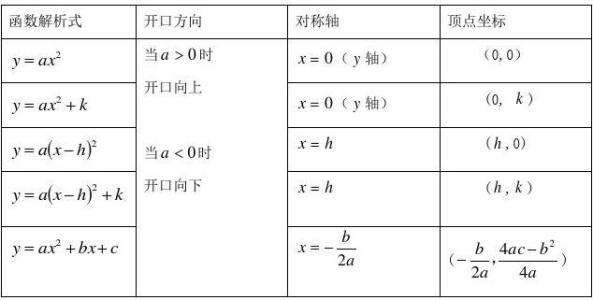
网络图片
四,用待定系数法确定二次函数的解析式的步骤
设,先设出二次函数的解析式,一般式y=ax²+bx+c、顶点式y=a(x+h)²+k、交点式y=a(x-x1)(x-x2)其中a≠0。
代,根据题中所给的条件,代入二次函数的解析式中,得到关于解析式中待定系数的方程组。
解,解此方程(组)求待定系数。
还原,将求出的待定系数还原解析式中。
五,抛物线的解析式的确定方法:一般式y=ax²+bx+c、顶点式y=a(x+h)²+k、交点式y=a(x-x1)(x-x2)其中a≠0。
考生们一定要熟练掌握这几种方法,根据题意正确选择采用哪种形式合适。
六,用合适观点看一元二次方程
(一)抛物线与直线的交点
1.抛物线y=抛物线y=ax²+bx+c与y轴的交点与y轴的交点是(0,c)
2.抛物线y=ax²+bx+c与x轴的交点,因为x轴上的点的纵坐标都是0,所以令y=0代入得ax²+bx+c=0
若△≥0,则这个抛物线与x轴有交点。
若△<0,则这个抛物线与x轴没有交点。
3.一次函数y=kx+b1(k≠0)的图像与二次函数y=ax²+bx+c(a≠0)的图像的交点由方程组y=kx+b1与y=ax²+bx+c联立的解的个数决定。
当方程组有两个不同的解时→两个函数有两个交点。
当方程组有两个相同的解时→两个函数有一个交点。
当方程组无解时→两个函数没有交点。
逆向也成立。
(二)二次函数y=ax²+bx+c与一元二次方程ax²+bx+c=0的关系
抛物线y=ax²+bx+c与x轴交点的横坐标x1、x2是一元二次方程ax²+bx+c=0的两个根。
△=b²-4ac决定抛物线与x轴交点的个数。
△>0→抛物线与x轴有两个交点。
△=0→抛物线与x轴有一个交点。
△<0→抛物线与x轴没有交点。
七,二次三项式、一元二次方程、二次函数、一元二次不等式之间的关系
当二次三项式为0时,便是一元二次方程,此时x的值是一元二次方程的解,也是二次函数的图像与x轴交点的横坐标。
当二次三项式大于0(或小于)时,便是一元二次不等式,即考虑x值在哪个范围内变化时为正或为负,若二次函数y=ax²+bx+c的图像在x轴上方(或下方),则ax²+bx+c>0(或<0),此时ax²+bx+c>0(或<0)的解集为全体实数或无解。
 加载中,请稍侯......
加载中,请稍侯......
精彩评论