谈谈圆模型的构造原理及常见考题

通过“构造圆模型求解几何题”是现今很重要的一种方法，尤其是中考前刷题必备技能之一，它可以巧妙的解决掉一部分号称中考热点的几何最值题，也可以解答一些涉及到折叠类的求解题，掌握后相当于你的武器库又多了一件威力强大的武器，考试中一旦条件适合，拿出来一击必中。

圆的最值问题模型：

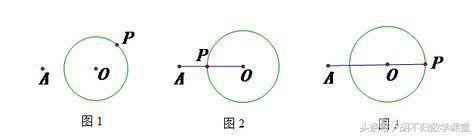
已知如图1，⊙O和圆外一点A，点P是⊙O上一点，求AP的最小值和最大值。

求AP最小值：连接AO交圆于点P,此时AP即是最小值，如图2；

求AP最大值：连接AO并延长交圆于点P,此时AP即是最大值，如图3。

其本质还是三角形的三边关系：任意两边之和大于第三边，任意两边只差小于第三边。

此模型还有点A在⊙O内部情况，解决方法和点A在⊙O外部情况类似，有兴趣的可以自己尝试画一画。

考试中的题型是千变万化的，试题中有些是已经给出了圆，有些没有需要自己构造出来圆，我们分别举例说明，先看今年的一道中考题：

【2018山东泰安12题】

如下图，⊙M的半径为2，圆心M的坐标为(3，4)，点P是⊙M上的任意一点，PA⊥PB，且PA、PB与轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为_______.

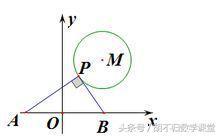
解析：本题已给出了圆，直接就可以按圆的最值模型求解。由题意得△PAB是直角三角形，点O是斜边AB上的中点，则OP就是AB的一半，所以求AB的最小值，就可以转化为求OP的最小值，什么时候OP最小？O点是⊙M外一定点，P点是⊙M上一动点，从条件上看已经符合圆的最值模型了。

如下图，当点O、P、M在同一直线上时，此时的线段OP有最小值，由点M的坐标可算得OM=5，又因为⊙M的半径为2，所以OP=3，故AB=6，即AB的最小值为6.

若试题中没有圆，但是具备隐形圆的条件，那就需要后天构造出辅助圆以达到解题的目的。下面详细谈一谈这种方法的原理及其应用技巧。

初中阶段达到构造圆的条件主要有下面3种情况：

①一定点一动点，两点间距离确定，则动点在圆上；②两定点一动点，满足以动点为顶点的角为90度，则动点在圆上；③直角三角形中，直角顶点固定，斜边运动但长度不变，则斜边中点在圆上。

理论依据：①是圆的定义：“平面上到定点的距离等于定长的所有点组成的图形，定点就是圆心，定长就是半径”；②和③是定理“直径所对的圆周角是直角；90°的圆周角所对的弦是直径”的实际应用。

与折叠相关

①折痕运动但过定点，则折叠后的对应点在圆上；②对应点确定，折痕为对应点连线的垂直平分线。

【典型例题】

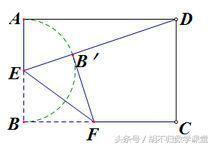
1、如下图，在矩形ABCD中，AB＝4，AD＝6，E是AB边的中点，F是线段BC上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是（ ）

A、2√10-2

B、6

C 、2√13-2

D、4

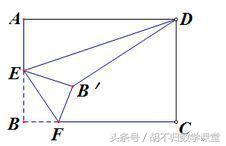
解析：翻折或者折叠的本质是轴对称，翻折后B的对应点为B＇，本题中E是定点，F是动点，属于构造圆的第①种情况，点B＇的轨迹在以点E为圆心EB长为半径的圆上（做题时只需作出在矩形ABCD内部的半圆即可）,如下图所示，作出辅助圆，连接ED与圆的交点即为符合题意的B＇，此时B′D就是最小值。在△AED中，AE=2，AD=6，由勾股定理得DE=2√10，又因为EB＇=EB=2，所以，B′D=DE-EB＇=2√10-2，故选A .

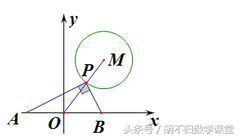
2、如下图，正方形ABCD中，AB=8，O为AB的中点，P为正方形ABCD外一动点，且AP⊥CP，则线段OP的最大值为（ ）

A.4+4√2

B.2＋4√2

C.4√2

D.6

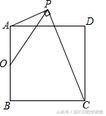
解析：点A、C是定点，P点为动点，且∠APC是直角，正好符合构造辅助圆的第②条件：“两定点一动点，满足以动点为顶点的角为90度，则动点在圆上”，以AC为直径作圆，则点A、B、C、D都在圆上，可以用圆模型中的最值问题解决，易得OP的最大值为OE+PE=4+4√2，自己动手试一试。

以上两题都是分两步走：①先构造出辅助圆；②再按照圆的最值模型求解。构造圆模型是求解几何综合题很重要的一种方法，过程中往往要涉及到诸如勾股定理、全等、相似、三角函数等知识。

怎么样？圆模型的构造原理以及借助圆模型解答最值问题的方法，你掌握了吗？