圆中的垂径定理
如图,设A、B是圆O的一条弦,P为AB的中点,则AB⊥OP,即:kAB·kOP=-1;
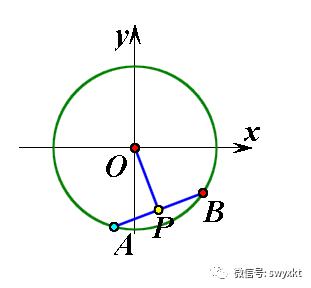
类比,在圆锥曲线中是否有相似的性质呢?
2.椭圆、双曲线中的垂径定理

思考:什么情况下适合使用这个结论?
本结论联系的弦的斜率与弦的中点坐标之间的关系,故涉及到两者有关的问题时,适合使用该结论解题。
Ps:相信同学们对“点差法”一点都不陌生,但能将点差法的运算过程跳过,而抽象出该结论直接用于解题的同学会少很多!“学无止境”,想得比别人多一点、深一点,你就会更有优势。
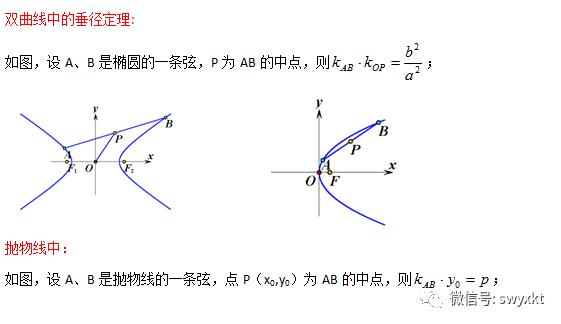
3.其它更多的结论
下面我们把弦AB往外平移到与圆O相切时,又有怎样的性质呢?
童鞋们自主完成吧,我提供一个框架给大家吧:
圆中:
如图,设直线l与圆O相切于点P,则l⊥OP,即:kl·kOP=-1;
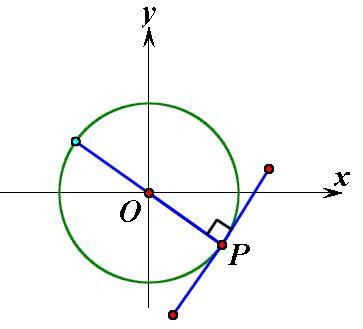
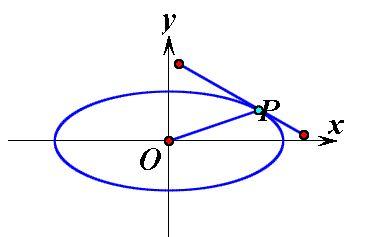

为更好的理解以上性质,可以从多角度思考结论怎么得来?比如我们知道当a=b时,椭圆就变成了圆,结论中的
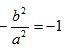
最后,我们的重点还是在于如何应用。请童鞋们自主思考:什么样的情况下,会利用得上这些结论帮助熟练、快速的解题呢?
4.应用举例,高考真题一例
一般解答过程:

利用椭圆的垂径定理的快速解答:
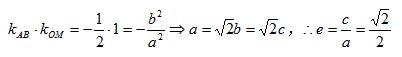

 加载中,请稍侯......
加载中,请稍侯......
精彩评论