已知函数的单调性，求参数的取值范围，我们先看看一下例题：

作图分析一下：

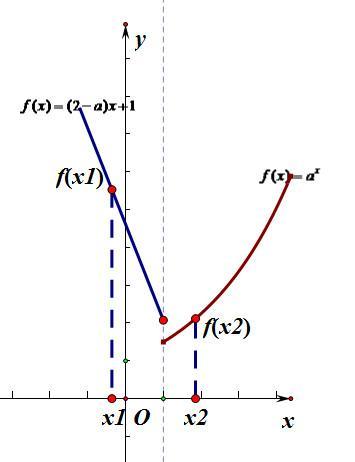
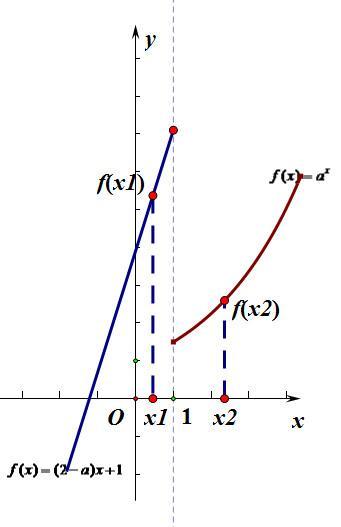
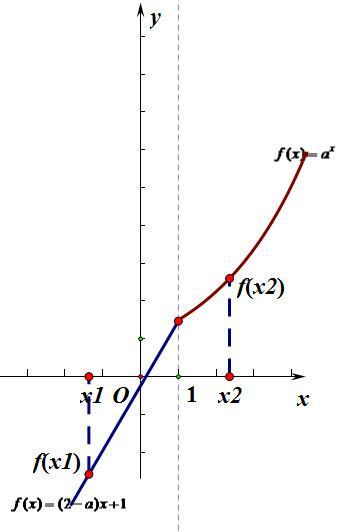
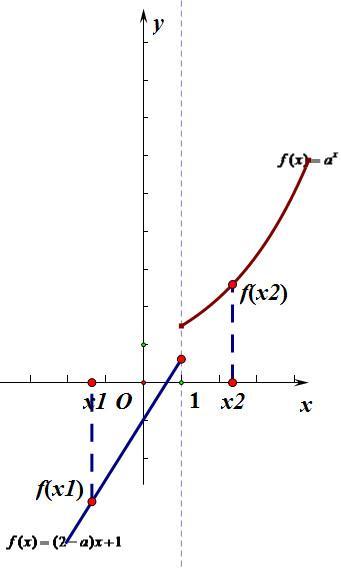
对照增函数的定义，我们可以清楚的知道，由上面四个图中，图（1）、图（2）不符合定义，舍去不要看了。图（3）、图（4）符合定义，细细观察这两幅图我们能发现一下共同点：分段函数的两段都增，且左边一段的最大值要小于等于右边一段的最小值。于是方法找到了，写出解题过程如下：

花括号中的第一个条件确定了左边的一次函数（直线）为增函数，第二个条件保证右边的函数（曲线）为增函数，第三个条件保证左边函数的最大值小于等于右边函数的最小值。

再看减函数的题目如何做：

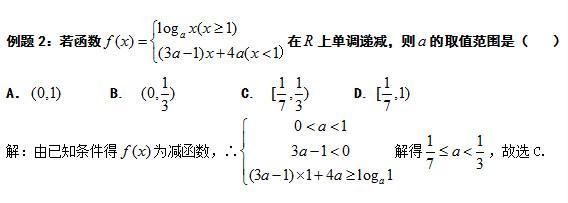
感觉以上两个题目的解析过程是不是一样的呢？

总结一下，我们需要注意两点：

一、函数整体和各个部分的单调性一致（统一）；

二、分界点（各个部分衔接的地方），按函数单调性不同，又分两种情况：

记住上面的结论

最后我们就是要多来几个题目强化一下，看看这样做题是不是很轻松了！